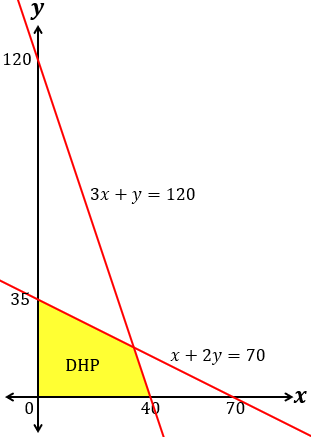
Untuk membuat satu buah roti A, diperlukan 50 g mentega dan 60 g tepung. Untuk membuat satu cetak roti B, diperlukan 100 g mentega dan 20 g tepung. Jika tersedia 3 , 5 kg mentega dan 2 , 4 kg tepung, maka jumlah roti A dan roti B terbanyak yang dapat dibuat adalah ... roti.

Pembahasan

Langkah 1 Misalkan menyatakan jumlah roti A dan menyatakan jumlah roti B.Ingat bahwa serta sehingga didapat sistem pertidaksamaan berikut ini. Langkah 2 Kemudian, fungsi objektifnya menyatakan jumlah roti terbanyak yang dapat dibuat, yaitu Langkah 3 Kemudian, gambarkan masing-masing garis x + 2 y = 70 dan 3 x + y = 120 dengan caratentukan terlebih dahulu titik potong masing-masing garis dengan sumbu- x dan sumbu- y . Untuk garis x + 2 y = 70 , didapatitik potongdengan sumbu- x dan sumbu- y sebagai berikut. x = 0 → y = 35 → ( 0 , 35 ) y = 0 → x = 70 → ( 70 , 0 ) Untuk garis 3 x + y = 120 , didapatitik potongdengan sumbu- x dan sumbu- y sebagai berikut. x = 0 → y = 120 → ( 0 , 120 ) y = 0 → x = 40 → ( 40 , 0 ) Kemudian, cari titik potong kedua garis tersebut seperti berikut. x + 2 y = 70 3 x + y = 120 ​ ∣ × 1 ∣ ∣ × 2 ∣ ​ x + 2 y = 70 6 x + 2 y = 240 − 5 x = − 170 x = 34 ​ ​ − Substitusi x = 34 ke salah satu persamaan, misal persamaan x + 2 y = 70. Akibatnya, didapat nilai y sebagai berikut. x + 2 y 34 + 2 y 34 + 2 y − 34 2 y 2 2 y ​ y ​ = = = = = = ​ 70 70 70 − 34 36 2 36 ​ 18 ​ Didapat bahwa titik potong kedua garis tersebut adalah ( 34 , 18 ) . Dengan demikian, daerah himpunan penyelesaian sistem pertidaksamaan di atas dapat digambarkan seperti berikut. Didapat bahwatitik pojoknya adalah ( 0 , 0 ) , dan ( 34 , 18 ) . Langkah 4 Substitusikan masing-masing titik pojok ke fungsi objektif f ( x , y ) = x + y untuk menentukan nilai maksimumnya. f ( 0 , 0 ) f ( 0 , 35 ) f ( 40 , 0 ) f ( 34 , 18 ) ​ = 0 + 0 = 0 + 35 = 40 + 0 = 34 + 18 ​ = 0 = 35 = 40 = 52 ​ Dengan demikian, roti terbanyak yang dapat dibuat adalah roti. Jadi, jawaban yang tepat adalah E.