Pertanyaan

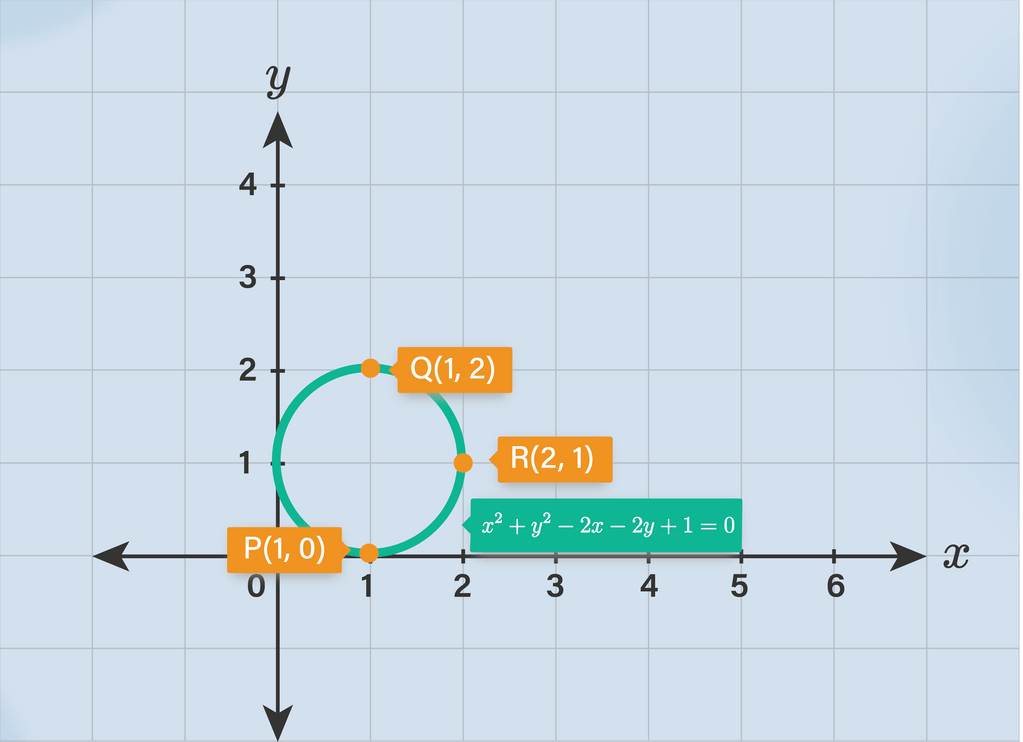
Tentukan persamaan lingkaran yang melalui tiga titik di bawah ini, kemudian gambar grafik lingkarannya: a. P ( 1 , 0 ) , Q ( 1 , 2 ) dan R ( 2 , 1 )

Tentukan persamaan lingkaran yang melalui tiga titik di bawah ini, kemudian gambar grafik lingkarannya:

a. $P (1, 0)$ , $Q (1, 2)$ dan $R (2, 1)$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

Y. Herlanda

Master Teacher

Mahasiswa/Alumni STKIP PGRI Jombang

Jawaban terverifikasi

Jawaban

persamaan lingkaran yang melalui tiga titik P ( 1 , 0 ) , Q ( 1 , 2 ) dan R ( 2 , 1 ) adalah x 2 + y 2 − 2 x − 2 y + 1 = 0 .

persamaan lingkaran yang melalui tiga titik

P (1, 0)

Q (1, 2)

dan

R (2, 1)

adalah

x^{2} + y^{2} - 2 x - 2 y + 1 = 0

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah x 2 + y 2 − 2 x − 2 y + 1 = 0 . Menentukan Persamaan Lingkaran yang Melalui Tiga Titik Persamaan lingkaran yang melalui tiga titik P ( 1 , 0 ) , Q ( 1 , 2 ) dan R ( 2 , 1 ) . Misalkan persamaan lingkaran: ( x − a ) 2 + ( y − b ) 2 = r 2 Titik P, Q, R terletak pada lingkaran, maka memenuhi persamaan: Untuk P ( 1 , 0 ) , maka: ( x − a ) 2 + ( y − b ) 2 ( 1 − a ) 2 + ( 0 − b ) 2 ( 1 − a ) 2 + ( − b ) 2 ( 1 − a ) 2 + b 2 = = = = r 2 r 2 r 2 r 2 ... ( 1 ) Untuk Q ( 1 , 2 ) , maka: ( x − a ) 2 + ( y − b ) 2 ( 1 − a ) 2 + ( 2 − b ) 2 = = r 2 r 2 ... ( 2 ) Untuk R ( 2 , 1 ) , maka: ( x − a ) 2 + ( y − b ) 2 ( 2 − a ) 2 + ( 1 − b ) 2 = = r 2 r 2 ... ( 3 ) Eliminasi persamaan (1) dan (2): ( 1 ) ( 2 ) : : ( 1 − a ) 2 ( 1 − a ) 2 b 2 b 2 b 2 b 2 + + − − − − − b 2 ( 2 − b ) 2 ( 2 − b ) 2 ( 2 − b ) ( 2 − b ) ( 4 − 2 b − 2 b + b 2 ) ( 4 − 4 b + b 2 ) ( 4 − 4 b ) 4 b b = = = = = = = = = r 2 r 2 0 0 0 0 0 4 1 − Substitusi b = 1 ke persamaan (1) dan (3): ( 1 ) ( 3 ) : : ( 1 − a ) 2 ( 1 − a ) 2 ( 1 − a ) 2 ( 2 − a ) 2 ( 2 − a ) 2 ( 2 − a ) 2 + + + + + + b 2 ( 1 ) 2 1 ( 1 − b ) 2 ( 1 − ( 1 ) ) 2 0 2 ( 2 − a ) 2 = = = = = = = r 2 r 2 r 2 r 2 r 2 r 2 r 2 Eliminasi: ( 1 − a ) 2 ( 2 − a ) 2 ( 1 − a ) 2 ( 1 − a ) ( 1 − a ) ( 1 − a − a + a 2 ) ( 1 − 2 a + a 2 ) − 3 + − − − − + 1 ( 2 − a ) 2 ( 2 − a ) ( 2 − a ) ( 4 − 2 a − 2 a + a 2 ) ( 4 − 4 a + a 2 ) 2 a 2 a + + + + + − 1 1 1 1 1 2 2 a a = = = = = = = = = = r 2 r 2 0 0 0 0 0 0 2 1 − Substitusikan a = 1 , b = 1 ke persamaan (1): ( 1 ) : ( 1 − a ) 2 ( 1 − 1 ) 2 0 2 + + + b 2 ( 1 ) 2 1 1 1 = = = = = r 2 r 2 r 2 r 2 r Dengan pusat lingkaran berada di titik ( a , b ) = ( 1 , 1 ) dan jari-jari lingkaran ( r ) = 1 . Diperoleh persamaan lingkaran sebagai berikut: ( x − a ) 2 + ( y − b ) 2 ( x − 1 ) 2 + ( y − 1 ) 2 ( x − 1 ) 2 + ( y − 1 ) 2 ( x − 1 ) ( x − 1 ) + ( y − 1 ) ( y − 1 ) ( x 2 − x − x + 1 ) + ( y 2 − y − y + 1 ) ( x 2 − 2 x + 1 ) + ( y 2 − 2 y + 1 ) − 1 x 2 + y 2 − 2 x − 2 y + 1 = = = = = = = r 2 ( 1 ) 2 1 1 1 0 0 Beriku adalah gambar grafik lingkaran berdasarkan persamaan di atas: Dengan demikian, persamaan lingkaran yang melalui tiga titik P ( 1 , 0 ) , Q ( 1 , 2 ) dan R ( 2 , 1 ) adalah x 2 + y 2 − 2 x − 2 y + 1 = 0 .

Jawaban yang benar untuk pertanyaan tersebut adalah $x^{2} + y^{2} - 2 x - 2 y + 1 = 0$ .

Menentukan Persamaan Lingkaran yang Melalui Tiga Titik

Persamaan lingkaran yang melalui tiga titik $P (1, 0)$ , $Q (1, 2)$ dan $R (2, 1)$ .

Misalkan persamaan lingkaran:

$(x - a)^{2} + (y - b)^{2} = r^{2}$

Titik P, Q, R terletak pada lingkaran, maka memenuhi persamaan:

Untuk $P (1, 0)$ , maka:

$(x - a)^{2} + (y - b)^{2} (1 - a)^{2} + (0 - b)^{2} (1 - a)^{2} + (- b)^{2} (1 - a)^{2} + b^{2} = = = = r^{2} r^{2} r^{2} r^{2} ... (1)$

Untuk $Q (1, 2)$ , maka:

$(x - a)^{2} + (y - b)^{2} (1 - a)^{2} + (2 - b)^{2} = = r^{2} r^{2} ... (2)$

Untuk $R (2, 1)$ , maka:

$(x - a)^{2} + (y - b)^{2} (2 - a)^{2} + (1 - b)^{2} = = r^{2} r^{2} ... (3)$

Eliminasi persamaan (1) dan (2):

$(1) (2) : : (1 - a)^{2} (1 - a)^{2} b^{2} b^{2} b^{2} b^{2} + + - - - - - b^{2} (2 - b)^{2} (2 - b)^{2} (2 - b) (2 - b) (4 - 2 b - 2 b + b^{2}) (4 - 4 b + b^{2}) (4 - 4 b) 4 b b = = = = = = = = = r^{2} r^{2} 0000041 -$

Substitusi $b = 1$ ke persamaan (1) dan (3):

$(1) (3) : : (1 - a)^{2} (1 - a)^{2} (1 - a)^{2} (2 - a)^{2} (2 - a)^{2} (2 - a)^{2} + + + + + + b^{2} (1)^{2} 1 (1 - b)^{2} (1 - (1))^{2} 0^{2} (2 - a)^{2} = = = = = = = r^{2} r^{2} r^{2} r^{2} r^{2} r^{2} r^{2}$

Eliminasi:

$(1 - a)^{2} (2 - a)^{2} (1 - a)^{2} (1 - a) (1 - a) (1 - a - a + a^{2}) (1 - 2 a + a^{2}) - 3 + - - - - + 1 (2 - a)^{2} (2 - a) (2 - a) (4 - 2 a - 2 a + a^{2}) (4 - 4 a + a^{2}) 2 a 2 a + + + + + - 111112 2 a a = = = = = = = = = = r^{2} r^{2} 00000021 -$

Substitusikan $a = 1, b = 1$ ke persamaan (1):

$(1) : (1 - a)^{2} (1 - 1)^{2} 0^{2} + + + b^{2} (1)^{2} 111 = = = = = r^{2} r^{2} r^{2} r^{2} r$

Dengan pusat lingkaran berada di titik $(a, b) = (1, 1)$ dan jari-jari lingkaran $(r) = 1$ . Diperoleh persamaan lingkaran sebagai berikut:

$(x - a)^{2} + (y - b)^{2} (x - 1)^{2} + (y - 1)^{2} (x - 1)^{2} + (y - 1)^{2} (x - 1) (x - 1) + (y - 1) (y - 1) (x^{2} - x - x + 1) + (y^{2} - y - y + 1) (x^{2} - 2 x + 1) + (y^{2} - 2 y + 1) - 1 x^{2} + y^{2} - 2 x - 2 y + 1 = = = = = = = r^{2} (1)^{2} 11100$

Beriku adalah gambar grafik lingkaran berdasarkan persamaan di atas:

Dengan demikian, persamaan lingkaran yang melalui tiga titik $P (1, 0)$ , $Q (1, 2)$ dan $R (2, 1)$ adalah $x^{2} + y^{2} - 2 x - 2 y + 1 = 0$ .

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.5 (8 rating)

JUSNIARI Zai

Pembahasan lengkap banget

Natasha Loani

. Ini yang aku cari!

Lucas

Jawaban tidak sesuai

Pertanyaan serupa

Diketahui sebuah lingkaran melalui titik ( 4 , 0 ) , titik ( 0 , 4 ) , dan titik asal. Tentukan: a. Pusat lingkaran. b. Jari-jari lingkaran. c. Persamaan lingkaran.

4.4

Jawaban terverifikasi

Lingkaran yang melalui titik-titik ( 4 , 2 ) , ( 1 , 3 ) dan ( − 3 , − 5 ) berjari-jari …

4.6

Jawaban terverifikasi

Tentukan persamaan lingkaran yang melalui tiga titik di bawah ini, kemudian gambar grafik lingkarannya: e. A ( 1 , 2 ) , B ( 4 , 6 ) dan C ( 1 , 6 )

4.8

Jawaban terverifikasi

Tentukan persamaan lingkaran yang melalui tiga titik di bawah ini, kemudian gambar grafik lingkarannya: c. K ( 2 , 5 ) , L ( 6 , 1 ) dan M ( 2 , 1 )

4.3

Jawaban terverifikasi

Tentukan persamaan lingkaran jika diketahui unsur-unsur berikut ini: j. Melalui titik-titik ( 4 , − 6 ) , ( 7 , − 3 ) dan ( 4 , 0 )