Pertanyaan

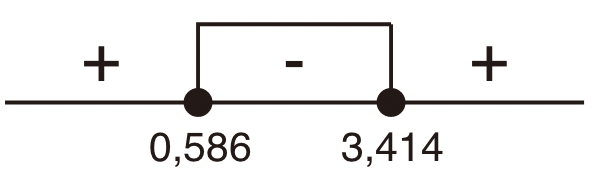
Tentukan penyelesaian dari pertidaksamaan berikut ini. Gunakan bantuan kalkulator untuk menentukan akar-akar dari persamaan kuadratnya. 2 x 2 − 8 x + 4 ≤ 0

Tentukan penyelesaian dari pertidaksamaan berikut ini. Gunakan bantuan kalkulator untuk menentukan akar-akar dari persamaan kuadratnya.

$2 x^{2} - 8 x + 4 \leq 0$

N. Puspita

Master Teacher

Jawaban terverifikasi

Pembahasan

Penyelesaian pertidaksamaan kuadrat dapat dicari dengan cara: Langkah pertama adalah menentukan akar-akar dari bentuk persamaan kuadratnya. Karena fungsi tidak dapat difaktorkan dengan cara pemfaktoran, maka, kita akan mencari akar-akar dari persamaan kuadratnya dengan rumus kuadratik atau rumus ABC. Ingat bahwa persamaan kuadrat mempunyai akar-akaryaitu . Maka, persamaan kuadrat mempunyai akar-akar: x = = = = 2 a − b ± b 2 − 4 ac 2 ⋅ 2 − ( − 8 ) ± ( − 8 ) 2 − 4 ⋅ 2 ⋅ 4 4 8 ± 64 − 32 4 8 ± 32 Dari rumus tersebut dan dengan bantuan kalkulator, diperoleh akar-akar, yaitu: dan Langkah berikutnya adalah menguji interval pada garis bilanganseperti pada gambar di bawah.Karena tanda pertidaksamaannya adalah tanda , maka daerah penyelesaian yang diambil adalah daerah . untuk x = 0 maka 2 ⋅ 0 2 − 8 ⋅ 0 + 4 = 4 (daerah di sebelah kiri)maka daerahkanannya bertandaselang-seling. Karena pertidaksamaannya menggunakan tanda , maka daerah penyelesaian yang diambil adalah daerah Jadi, penyelesaiannya adalah .

Penyelesaian pertidaksamaan kuadrat 2 x squared minus 8 x plus 4 less or equal than 0 dapat dicari dengan cara:

Langkah pertama adalah menentukan akar-akar dari bentuk persamaan kuadratnya. Karena fungsi f left parenthesis x right parenthesis equals 2 x squared minus 8 x plus 4 tidak dapat difaktorkan dengan cara pemfaktoran, maka, kita akan mencari akar-akar dari persamaan kuadratnya dengan rumus kuadratik atau rumus ABC. Ingat bahwa persamaan kuadrat straight a x squared plus straight b x plus straight c equals 0 mempunyai akar-akar yaitu $x equals fraction numerator negative straight b plus-or-minus square root of straight b squared minus 4 ac end root over denominator 2 straight a end fraction$ .

Maka, persamaan kuadrat 2 x squared minus 8 x plus 4 equals 0 mempunyai akar-akar:

$x = = = = \frac{- b \pm b ^{2} - 4 ac}{2 a} \frac{- ( - 8 ) \pm ( - 8 ) ^{2} - 4 \cdot 2 \cdot 4}{2 \cdot 2} \frac{8 \pm 64 - 32}{4} \frac{8 \pm 32}{4}$

Dari rumus tersebut dan dengan bantuan kalkulator, diperoleh akar-akar, yaitu:

$table attributes columnalign right center left columnspacing 0px end attributes row cell x subscript 1 end cell equals cell fraction numerator 8 plus square root of 96 over denominator 4 end fraction end cell row blank approximately equal to cell 3 comma 414 end cell end table$

dan

$table attributes columnalign right center left columnspacing 0px end attributes row cell x subscript 2 end cell equals cell fraction numerator 8 minus square root of 96 over denominator 4 end fraction end cell row blank approximately equal to cell 0 comma 586 end cell end table$

Langkah berikutnya adalah menguji interval pada garis bilangan seperti pada gambar di bawah. Karena tanda pertidaksamaannya adalah tanda less or equal than , maka daerah penyelesaian yang diambil adalah daerah minus .

untuk $x = 0 maka 2 \cdot 0^{2} - 8 \cdot 0 + 4 = 4$ (daerah di sebelah kiri) maka daerah kanannya bertanda selang-seling.

Karena pertidaksamaannya menggunakan tanda less than , maka daerah penyelesaian yang diambil adalah daerah minus
Jadi, penyelesaiannya adalah 0 comma 586 less or equal than x less or equal than 3 comma 414 .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

1.0 (1 rating)

Sopiansyah

Pembahasan tidak menjawab soal

Pertanyaan serupa

Tentukan penyelesaian dari pertidaksamaan x 2 + 3 x + 1 < 0 .

105

5.0

Jawaban terverifikasi

Tentukan himpunan penyelesaian dari − 2 x 2 − 3 x + 3 ≥ 0 .

0.0

Jawaban terverifikasi

Batas-batas nilai k agar ( k + 2 ) x 2 − 2 k x + ( 2 − k ) bernilai positif untuk setiap x ∈ R adalah ....

0.0

Jawaban terverifikasi

Tentukan penyelesaian dari pertidaksamaan berikut ini. Gunakan bantuan kalkulator untuk menentukan akar-akar dari persamaan kuadratnya. 3 x 2 + 4 x − 8 ≥ 0

0.0

Jawaban terverifikasi

Batas-batas nilai k agar bernilai negatif untuk setiap x ∈ R adalah .....

0.0

Jawaban terverifikasi