Tentukan nilai n agar garis yang diberikan dapat: b. memotong di dua titik yang berlainan, serta x 2 + y 2 = 4 ; y = n x 2 + y 2 + 2 y − 1 = 0 ; y = x − n

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah nilai n agar garis y = n dapat memotong lingkaran x 2 + y 2 = 4 di duatitik yang berlainan adalah − 2 < n < 2 dannilai n agar garis y = x − n dapat memotong lingkaran x 2 + y 2 + 2 y − 1 = 0 di duatitik yang berlainan adalah n < − 1 a t a u n > 3 . Ingat! Hubungan antara garis g dan lingkaran L dapat ditentukan dari nilai diskriminan berdasarkan persamaan kuadrat yang diperoleh saat mesubstitusikan persamaan garis ke dalam persamaan lingkaran. Rumus mencari nilai diskriminan adalah: D = b 2 − 4 a c Jika D > 0 , garis g memotong lingkaran L di dua titik yang berbeda. Jika D = 0 , garis g menyinggunglingkaran L di satu titik. Jika D < 0 , garis g tidak memotong lingkaran L . a.Garis memotong di duatitik yang berlainan dengan syarat D > 0 maka nilai n dapat dihitung sebagai berikut. Pertama akan dicari nilai n pada lingkaran x 2 + y 2 = 4 dan garis y = n . Substitusi garis y = n ke dalam lingkaran x 2 + y 2 = 4 . x 2 + y 2 x 2 + n 2 − 4 ​ = = ​ 4 0 ​ Diperoleh a = 1 , b = 0 , dan c = n 2 − 4 , sehingga dapat dihitung nilai diskriminan sebagai berikut: D ​ = = = ​ b 2 − 4 a c 0 2 − 4 ( 1 ) ( n 2 − 4 ) − 4 n 2 + 16 ​ Syarat garis memotong lingkaran di satu titik adalah D > 0 , sehingga diperoleh − 4 n 2 + 16 > 0 . Untuk − 4 n 2 + 16 = 0 diperoleh n = 2 atau n = − 2 . 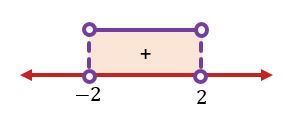Untuk menentukan daerah penyelesaian menggunakan garis bilangan seperti berikut: Daerah yang memenuhi adalah daerah yang bernilai positif, sehingga nilai n yang memenuhi adalah − 2 < n < 2 . Kedua akan dicari nilai n pada lingkaran x 2 + y 2 + 2 y − 1 = 0 dan garis y = x − n . Substitusi garis y = x − n ⇔ x = y + n ke dalam lingkaran x 2 + y 2 + 2 y − 1 = 0 . x 2 + y 2 + 2 y − 1 ( y + n ) 2 + y 2 + 2 y − 1 y 2 + 2 n y + n 2 + y 2 + 2 y − 1 2 y 2 + ( 2 n + 2 ) y + ( n 2 − 1 ) ​ = = = = ​ 0 0 0 0 ​ Diperoleh a = 2 , b = 2 n + 2 , dan c = n 2 − 1 , sehingga dapat dihitung nilai diskriminan sebagai berikut: D ​ = = = = ​ b 2 − 4 a c ( 2 n + 2 ) 2 − 4 ( 2 ) ( n 2 − 1 ) − 4 n 2 + 8 n + 12 n 2 − 2 n − 3 ​ Syarat garis memotong lingkaran di satu titik adalah D > 0 , sehingga diperoleh n 2 − 2 n − 3 > 0 . Untuk n 2 − 2 n − 3 = 0 diperoleh n = 3 atau n = − 1 . 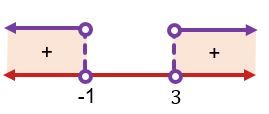Untuk menentukan daerah penyelesaian menggunakan garis bilangan seperti berikut: Daerah yang memenuhi adalah daerah yang bernilai positif, sehingga nilai n yang memenuhi adalah n < − 1 atau n > 3 . Dengan demikian,nilai n agar garis y = n dapat memotong lingkaran x 2 + y 2 = 4 di duatitik yang berlainan adalah − 2 < n < 2 dannilai n agar garis y = x − n dapat memotong lingkaran x 2 + y 2 + 2 y − 1 = 0 di duatitik yang berlainan adalah n < − 1 atau n > 3 .