Pertanyaan

Tentukan himpunan penyelesaian persamaan 1 − sin ( 2 x + 4 1 π ) = 0 , 5 pada interval 0 ≤ x ≤ 2 π .

Tentukan himpunan penyelesaian persamaan $1 - sin (2 x + \frac{1}{4} π) = 0, 5$ pada interval $0 \leq x \leq 2 π$ .

S. Nur

Master Teacher

Jawaban terverifikasi

Jawaban

himpunan penyelesaian persamaan pada interval adalah HP = { 24 7 π , 24 23 π , 1 24 7 π , 1 24 23 π } .

himpunan penyelesaian persamaan 1 minus sin open parentheses 2 x plus 1 fourth straight pi close parentheses equals 0 comma 5

pada interval 0 less or equal than x less or equal than 2 straight pi

adalah

HP = {\frac{7}{24} π, \frac{23}{24} π, 1 \frac{7}{24} π, 1 \frac{23}{24} π}

Pembahasan

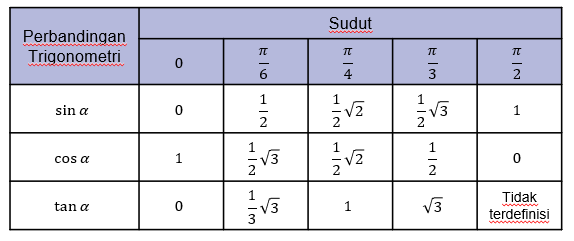
Diketahui ekuivalen dengan 1 − sin ( 2 x + 4 1 π ) 1 − 0 , 5 0 , 5 2 1 sin ( 2 x + 4 1 π ) = = = = = 0 , 5 sin ( 2 x + 4 1 π ) sin ( 2 x + 4 1 π ) sin ( 2 x + 4 1 π ) 2 1 Ingat kembali nilai trigonometri pada sudut istimewa seperti pada tabel di bawah ini. Berdasarkan tabel di atas, diperoleh bahwa s in 6 π = 2 1 sehingga diperoleh sebagai berikut. sin ( 2 x + 4 1 π ) sin ( 2 x + 4 1 π ) = = 2 1 sin 6 π maka 2 x + 4 1 π 2 x 2 x 2 x x = = = = = 6 π + k ⋅ 2 π 6 π − 4 1 π + k ⋅ 2 π 12 2 π − 12 3 π + k ⋅ 2 π − 12 1 π + k ⋅ 2 π − 24 π + k ⋅ π atau 2 x + 4 1 π 2 x + 4 1 π 2 x + 4 1 π 2 x 2 x 2 x x = = = = = = = ( π − 6 π ) + k ⋅ 2 π ( 6 6 π − 6 π ) + k ⋅ 2 π 6 5 π + k ⋅ 2 π 6 5 π − 4 1 π + k ⋅ 2 π 12 10 π − 12 3 π + k ⋅ 2 π 12 7 π + k ⋅ 2 π 24 7 π + k ⋅ π dengan k merupakan bilangan bulat. Kemudian uji berbagai nilai k , dan cari nilai x yang memenuhi interval 0 ≤ x ≤ 2 π . Untuk x = − 24 π + k ⋅ π k = 0 → k = 1 → k = 2 → k = − 1 → x = − 24 π + 0 ⋅ π x = − 24 π + 0 x = − 24 π x = − 24 π + 1 ⋅ π x = − 24 π + π x = 24 23 π x = − 24 π + 2 ⋅ π x = − 24 π + 2 π x = 24 47 π x = 1 24 23 π x = − 24 π + ( − 1 ) ⋅ π x = − 24 π − π x = − 1 24 1 π ( tidak memenuhi ) ( memenuhi ) ( memenuhi ) ( tidak memenuhi ) Untuk x = 24 7 π + k ⋅ π k = 0 → k = 1 → k = 2 → k = − 1 → x = 24 7 π + 0 ⋅ π x = 24 7 π + 0 x = 24 7 π x = 24 7 π + 1 ⋅ π x = 24 7 π + π x = 1 24 7 π x = − 24 π + 2 ⋅ π x = 24 7 π + 2 π x = 2 24 7 π x = 24 7 π + ( − 1 ) ⋅ π x = 24 7 π − π x = − 24 17 π ( memenuhi ) ( memenuhi ) ( tidak memenuhi ) ( tidak memenuhi ) Jadihimpunan penyelesaian persamaan pada interval adalah HP = { 24 7 π , 24 23 π , 1 24 7 π , 1 24 23 π } .

Diketahui 1 minus sin open parentheses 2 x plus 1 fourth straight pi close parentheses equals 0 comma 5 ekuivalen dengan

$1 - sin (2 x + \frac{1}{4} π) 1 - 0, 5 0, 5 \frac{1}{2} sin (2 x + \frac{1}{4} π) = = = = = 0, 5 sin (2 x + \frac{1}{4} π) sin (2 x + \frac{1}{4} π) sin (2 x + \frac{1}{4} π) \frac{1}{2}$

Ingat kembali nilai trigonometri pada sudut istimewa seperti pada tabel di bawah ini.

Berdasarkan tabel di atas, diperoleh bahwa $s in \frac{π}{6} = \frac{1}{2}$ sehingga table attributes columnalign right center left columnspacing 0px end attributes row cell sin open parentheses 2 x plus 1 fourth straight pi close parentheses end cell equals cell 1 half end cell end table diperoleh sebagai berikut.

$sin (2 x + \frac{1}{4} π) sin (2 x + \frac{1}{4} π) = = \frac{1}{2} sin \frac{π}{6}$

maka

$2 x + \frac{1}{4} π 2 x 2 x 2 x x = = = = = \frac{π}{6} + k \cdot 2 π \frac{π}{6} - \frac{1}{4} π + k \cdot 2 π \frac{2}{12} π - \frac{3}{12} π + k \cdot 2 π - \frac{1}{12} π + k \cdot 2 π - \frac{π}{24} + k \cdot π$

atau

$2 x + \frac{1}{4} π 2 x + \frac{1}{4} π 2 x + \frac{1}{4} π 2 x 2 x 2 x x = = = = = = = (π - \frac{π}{6}) + k \cdot 2 π (\frac{6}{6} π - \frac{π}{6}) + k \cdot 2 π \frac{5}{6} π + k \cdot 2 π \frac{5}{6} π - \frac{1}{4} π + k \cdot 2 π \frac{10}{12} π - \frac{3}{12} π + k \cdot 2 π \frac{7}{12} π + k \cdot 2 π \frac{7 π}{24} + k \cdot π$

dengan $k$ merupakan bilangan bulat.

Kemudian uji berbagai nilai $k$ , dan cari nilai $x$ yang memenuhi interval $0 \leq x \leq 2 π$ .

Untuk $x = - \frac{π}{24} + k \cdot π$

$k = 0 \to k = 1 \to k = 2 \to k = - 1 \to x = - \frac{π}{24} + 0 \cdot π x = - \frac{π}{24} + 0 x = - \frac{π}{24} x = - \frac{π}{24} + 1 \cdot π x = - \frac{π}{24} + π x = \frac{23 π}{24} x = - \frac{π}{24} + 2 \cdot π x = - \frac{π}{24} + 2 π x = \frac{47 π}{24} x = 1 \frac{23}{24} π x = - \frac{π}{24} + (- 1) \cdot π x = - \frac{π}{24} - π x = - 1 \frac{1}{24} π (tidak memenuhi) (memenuhi) (memenuhi) (tidak memenuhi)$

Untuk $x = \frac{7 π}{24} + k \cdot π$

$k = 0 \to k = 1 \to k = 2 \to k = - 1 \to x = \frac{7 π}{24} + 0 \cdot π x = \frac{7 π}{24} + 0 x = \frac{7 π}{24} x = \frac{7 π}{24} + 1 \cdot π x = \frac{7 π}{24} + π x = 1 \frac{7}{24} π x = - \frac{π}{24} + 2 \cdot π x = \frac{7 π}{24} + 2 π x = 2 \frac{7 π}{24} x = \frac{7 π}{24} + (- 1) \cdot π x = \frac{7 π}{24} - π x = - \frac{17}{24} π (memenuhi) (memenuhi) (tidak memenuhi) (tidak memenuhi)$

Jadi himpunan penyelesaian persamaan 1 minus sin open parentheses 2 x plus 1 fourth straight pi close parentheses equals 0 comma 5 pada interval 0 less or equal than x less or equal than 2 straight pi adalah $HP = {\frac{7}{24} π, \frac{23}{24} π, 1 \frac{7}{24} π, 1 \frac{23}{24} π}$ .