Diketahui  maka berdasarkan identitas trigonometri yaitu
maka berdasarkan identitas trigonometri yaitu  maka
maka  sehingga diperoleh sebagai berikut.
sehingga diperoleh sebagai berikut.
2sin2x+3cos x2(1−cos2x)+3cos x2−2cos2x+3cos x2cos2x−3cos x−2====000 (kedua ruas dikali−1)0
Misalkan  maka
maka

Nilai maksimum cosinus adalah  maka tidak ada nilai
maka tidak ada nilai  yang memenuhi
yang memenuhi  .
.
ingat kembali nilai trigonometri pada sudut istimewa seperti pada tabel di bawah ini.
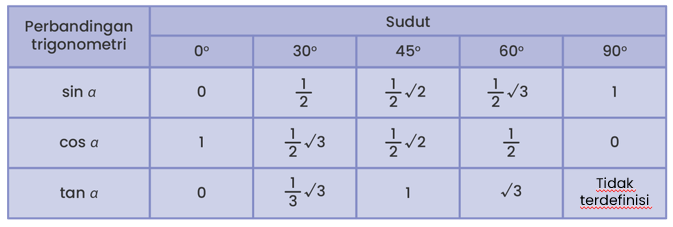
Berdasarkan tabel diperoleh bahwa  .
.
Karena  terletak pada interval
terletak pada interval  dan cosinus bernilai negatif terdapat pada kuadran II dan III maka nilai cosinus yang memenuhi persamaan adalah nilai cosinus pada kuadran II dengan rumus sudut
dan cosinus bernilai negatif terdapat pada kuadran II dan III maka nilai cosinus yang memenuhi persamaan adalah nilai cosinus pada kuadran II dengan rumus sudut  . Menurut sudut berelasi pada kuadran II yaitu cos (180∘−α)=−cos α.
. Menurut sudut berelasi pada kuadran II yaitu cos (180∘−α)=−cos α.
cos xcos xcos xcos x==== −21−cos 60∘cos(180∘−60∘)cos 120∘
Penyelesaian persamaan cosinus.
cos x=cos 120∘x=±120∘+k⋅360∘
dengan k merupakan bilangan bulat.
Selanjutnya, menentukan nilai x yang sesuai interval dengan mencoba berbagai nilai k.
k=0 →k=1 →k=−1 →x=±120∘+0⋅360∘x=±120∘+0x=120∘x=±120∘+1⋅360∘x=±120∘+360∘x=480∘x=±120∘−1⋅360∘x=±120∘−360∘x=−240∘∨∨∨x=−120∘x=240∘x=−480∘
Karena  terletak pada
terletak pada  maka nilai x yang memenuhi persamaan
maka nilai x yang memenuhi persamaan  adalah
adalah  .
.
Jadi nilai x yang memenuhi persamaan  adalah
adalah  .
.
Oleh karena itu, jawaban yang benar adalah C.


















