Tentukan Q 1 , ​ Q 2 , ​ dan Q 3 ​ dari data di samping!

Pembahasan

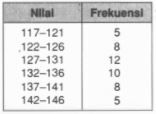
Ingat bahwa: Untuk mencari kuartil pada data kelompok dapat digunakan rumus berikut. Q i ​ = L Q i ​ ​ + f Q i ​ ​ 4 i ​ n − f k ​ ​ × p dengan Q i ​ L Q i ​ ​ i n f k ​ f Q i ​ ​ p ​ = = = = = = = ​ kuartil ke − i tepi bawah kelas kuartil 1 , 2 , 3 banyak data frekuensi kumulatif sebelum kelas kuartil frekuensi kelas kuartil panjang kelas ​ Berdasarkan soal di atas diperoleh banyak data adalah n = 5 + 8 + 12 + 10 + 8 + 5 = 48 . Kuartil 1: Q 1 ​ ​ = = = ​ data ke − 4 1 ​ n data ke − 4 1 ​ × 48 data ke − 12 ​ Sehingga diperoleh Q 1 ​ data ke- 12 pada interval 122 − 126 . L Q 1 ​ ​ = 122 − 0 , 5 = 121 , 5 f k ​ = 5 f Q 1 ​ ​ = 8 p = 122 − 117 = 5 Q 1 ​ ​ = = = = = = ​ L Q i ​ ​ + f Q 1 ​ ​ 4 1 ​ n − f k ​ ​ × p 121 , 5 + 8 12 − 5 ​ × 5 121 , 5 + 8 7 ​ × 5 121 , 5 + 8 35 ​ 121 , 5 + 4 , 375 125 , 875 ​ Kuartil 2: Q 2 ​ ​ = = = ​ data ke − 4 2 ​ n data ke − 4 2 ​ × 48 data ke − 24 ​ Sehingga diperoleh Q 2 ​ data ke- 24 pada interval 127 − 131 . L Q 2 ​ ​ = 127 − 0 , 5 = 126 , 5 f k ​ = 5 + 8 = 13 f Q 2 ​ ​ = 12 p = 122 − 117 = 5 Q 2 ​ ​ = = = = = = ​ L Q 2 ​ ​ + f Q 2 ​ ​ 4 2 ​ n − f k ​ ​ × p 126 , 5 + 12 24 − 13 ​ × 5 126 , 5 + 12 11 ​ × 5 126 , 5 + 12 55 ​ 126 , 5 + 4 , 58 131 , 08 ​ Kuartil 3: Q 3 ​ ​ = = = ​ data ke − 4 3 ​ n data ke − 4 3 ​ × 48 data ke − 36 ​ Sehingga diperoleh Q 3 ​ data ke- 36 pada interval 137 − 141 . L Q 3 ​ ​ = 137 − 0 , 5 = 136 , 5 f k ​ = 5 + 8 + 12 + 10 = 35 f Q 3 ​ ​ = 8 p = 122 − 117 = 5 Q 3 ​ ​ = = = = = = ​ L Q 3 ​ ​ + f Q 3 ​ ​ 4 3 ​ n − f k ​ ​ × p 136 , 5 + 8 36 − 35 ​ × 5 136 , 5 + 8 1 ​ × 5 136 , 5 + 8 5 ​ 136 , 5 + 0 , 625 137 , 125 ​ Dengan demikian, diperoleh kuartil pertamanya 125 , 875 , kuartil keduanya 131 , 08 , dan kuartil ketiganya adalah 137 , 125 .