Tentukan median dan kuartil dari data yang dinyatakan dengan histogram berikut.

Pembahasan

Ingat kembali rumus kuartil bawah ( Q 1 ​ ) , median ( Q 2 ​ ) , dan kuartil atas ( Q 3 ​ ) pada data berkelompok sebagai berikut: Q 1 ​ = L 1 ​ + c ⎝ ⎛ ​ f 1 ​ 4 1 ​ n − F 1 ​ ​ ⎠ ⎞ ​ Q 2 ​ = L 2 ​ + c ⎝ ⎛ ​ f 2 ​ 2 1 ​ n − F 2 ​ ​ ⎠ ⎞ ​ Q 3 ​ = L 3 ​ + c ⎝ ⎛ ​ f 3 ​ 4 3 ​ n − F 3 ​ ​ ⎠ ⎞ ​ dimana L 1 , 2 , 3 ​ = tepi bawah kelas kuartil bawah, median, kuartil atas n = ukuran data (jumlah frekuensi) f 1 , 2 , 3 ​ = frekuensi pada interval kelas kuartil bawah, median dan kuartil atas F 1 , 2 , 3 ​ = frekuensi kumulatif sebelum kelas kuartil bawah, median dan kuartil atas c = panjang kelas 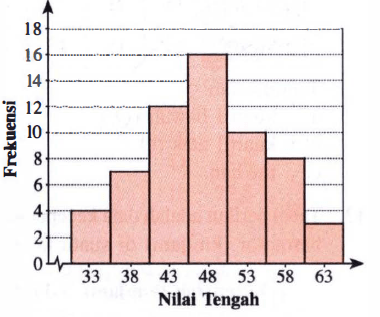Oleh karena itu, berdasarkan histogram di atas dapat dibuatkan tabel distribusi frekuensi di bawah ini 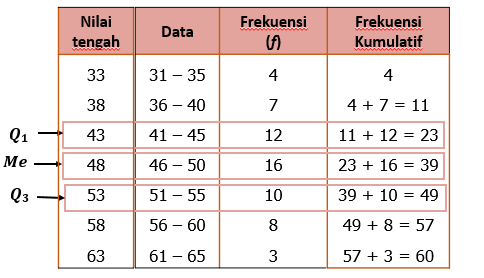Interval kelas kuartil bawahterletak pada 41 − 45 diperoleh dari 4 1 ​ n = 4 1 ​ × 60 = 15 (lihat dari frekuensi kumulatif), dengan n = 60 , L 1 ​ = 41 − 0 , 5 = 40 , 5 , f 1 ​ = 12 , F 1 ​ = 11 , c = 5 Q 1 ​ ​ = = = = = ​ L 1 ​ + c ⎝ ⎛ ​ f 1 ​ 4 1 ​ n − F 1 ​ ​ ⎠ ⎞ ​ 40 , 5 + 5 ⋅ ⎝ ⎛ ​ 12 4 1 ​ ⋅ 60 − 11 ​ ⎠ ⎞ ​ 40 , 5 + 5 ⋅ ( 12 15 − 11 ​ ) 40 , 5 + 1 , 67 42 , 17 ​ Interval kelas medianterletak pada 46 − 50 diperoleh dari 2 1 ​ n = 2 1 ​ × 60 = 30 (lihat dari frekuensi kumulatif), dengan n = 60 , L 2 ​ = 46 − 0 , 5 = 45 , 5 , f 2 ​ = 16 , F 2 ​ = 23 , c = 5 Q 2 ​ ​ = = = = = ​ L 2 ​ + c ⎝ ⎛ ​ f 2 ​ 2 1 ​ n − F 2 ​ ​ ⎠ ⎞ ​ 45 , 5 + 5 ⋅ ⎝ ⎛ ​ 16 2 1 ​ ⋅ 60 − 23 ​ ⎠ ⎞ ​ 45 , 5 + 5 ⋅ ( 16 30 − 23 ​ ) 45 , 5 + 2 , 19 47 , 69 ​ Interval kelas kuartil atas terletak pada 51 − 55 diperoleh dari 4 3 ​ n = 4 3 ​ × 60 = 45 (lihat dari frekuensi kumulatif), dengan n = 60 , L 3 ​ = 51 − 0 , 5 = 50 , 5 , f 3 ​ = 10 , F 3 ​ = 39 , c = 5 Q 3 ​ ​ = = = = = ​ L 3 ​ + c ⎝ ⎛ ​ f 3 ​ 4 3 ​ n − F 3 ​ ​ ⎠ ⎞ ​ 50 , 5 + 5 ⋅ ⎝ ⎛ ​ 10 4 3 ​ ⋅ 60 − 39 ​ ⎠ ⎞ ​ 50 , 5 + 5 ⋅ ( 10 45 − 39 ​ ) 50.5 + 3 53 , 5 ​ Dengan demikian, kuartil bawah Q 1 ​ = 42 , 17 , median Q 2 ​ = 47 , 69 , dan kuartil atas Q 3 ​ = 53 , 5 .