Tabel berikut merupakan ukuran berat paket pos dalam suatu pengiriman melalui bandara Soekarno-Hatta. Hitunglah nilai dari median, kuartil bawah dan kuartil atas.

Pertanyaan

Tabel berikut merupakan ukuran berat paket pos dalam suatu pengiriman melalui bandara Soekarno-Hatta.

Hitunglah nilai dari median, kuartil bawah dan kuartil atas.

M. Mariyam

Master Teacher

Mahasiswa/Alumni Institut Pertanian Bogor

Jawaban terverifikasi

Pembahasan

Ingat kembali rumus kuartil bawah $\left(Q_1\right)$ , median $\left(Q_2\right)$ , dan kuartil atas $\left(Q_3\right)$ pada data berkelompok sebagai berikut:

$Q subscript 1 equals L subscript 1 plus c open parentheses fraction numerator begin display style 1 fourth end style n minus F subscript 1 over denominator f subscript 1 end fraction close parentheses Q subscript 2 equals L subscript 2 plus c open parentheses fraction numerator begin display style 1 half n minus F subscript 2 end style over denominator f subscript 2 end fraction close parentheses Q subscript 3 equals L subscript 3 plus c open parentheses fraction numerator begin display style 3 over 4 n minus F subscript 3 end style over denominator f subscript 3 end fraction close parentheses$

dimana

$L_{1,2,3}=$ tepi bawah kelas kuartil bawah, median, kuartil atas

$n=$ ukuran data (jumlah frekuensi)

$f_{1,2,3}=$ frekuensi pada interval kelas kuartil bawah, median dan kuartil atas

$F_{1,2,3}=$ frekuensi kumulatif sebelum kelas kuartil bawah, median dan kuartil atas

$c=$ panjang kelas

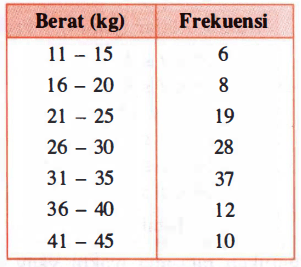
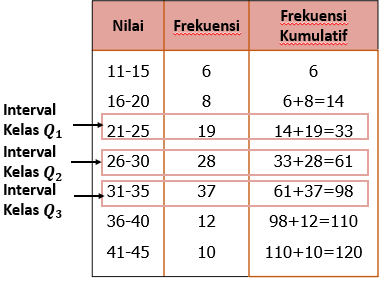
Oleh karena itu, berdasarkan tabel distribusi frekuensi di atas, kita menambahkan satu kolom yaitu frekuensi kumulatif seperti pada tabel di bawah ini

Interval kelas kuartil bawah terletak pada $21-25$ diperoleh dari $\frac14n=\frac14\times120=30$ (lihat dari frekuensi kumulatif), dengan

$n=120,\;\;L_1=21-0,5=20,5,\;\;f_1=19,\;\;F_1=14,\;\;c=5$

$table attributes columnalign right center left columnspacing 0px end attributes row cell Q subscript 1 end cell equals cell L subscript 1 plus c open parentheses fraction numerator begin display style 1 fourth end style n minus F subscript 1 over denominator f subscript 1 end fraction close parentheses end cell row blank equals cell 20 comma 5 plus 5 times open parentheses fraction numerator begin display style 1 fourth end style times 120 minus 14 over denominator 19 end fraction close parentheses end cell row blank equals cell 20 comma 5 plus 5 times open parentheses fraction numerator begin display style 30 minus 14 end style over denominator 19 end fraction close parentheses end cell row blank equals cell 20 comma 5 plus 4 comma 21 end cell row blank equals cell 24 comma 71 end cell end table$

Interval kelas median terletak pada $26-30$ diperoleh dari $\frac12n=\frac12\times120=60$ (lihat dari frekuensi kumulatif), dengan

$n=120,\;\;L_2=26-0,5=25,5,\;\;f_2=28,\;\;F_2=33,\;\;c=5$

$table attributes columnalign right center left columnspacing 0px end attributes row cell Q subscript 2 end cell equals cell L subscript 2 plus c open parentheses fraction numerator begin display style 1 half end style n minus F subscript 2 over denominator f subscript 2 end fraction close parentheses end cell row blank equals cell 25 comma 5 plus 5 times open parentheses fraction numerator begin display style 1 half end style times 120 minus 33 over denominator 28 end fraction close parentheses end cell row blank equals cell 25 comma 5 plus 5 times open parentheses fraction numerator begin display style 60 minus 33 end style over denominator 28 end fraction close parentheses end cell row blank equals cell 25 comma 5 plus 4 comma 82 end cell row blank equals cell 30 comma 32 end cell end table$

Interval kelas kuartil atas terletak pada $31-35$ diperoleh dari $\frac34n=\frac34\times120=90$ (lihat dari frekuensi kumulatif), dengan

$n=120,\;\;L_3=31-0,5=30,5,\;\;f_3=37,\;\;F_3=61,\;\;c=5$

$table attributes columnalign right center left columnspacing 0px end attributes row cell Q subscript 3 end cell equals cell L subscript 3 plus c open parentheses fraction numerator begin display style 3 over 4 end style n minus F subscript 3 over denominator f subscript 3 end fraction close parentheses end cell row blank equals cell 30 comma 5 plus 5 times open parentheses fraction numerator begin display style 3 over 4 end style times 120 minus 61 over denominator 37 end fraction close parentheses end cell row blank equals cell 30 comma 5 plus 5 times open parentheses fraction numerator begin display style 90 minus 61 end style over denominator 37 end fraction close parentheses end cell row blank equals cell 30 comma 5 plus 3 comma 92 end cell row blank equals cell 34 comma 42 end cell end table$

Dengan demikian, kuartil bawah $Q_1=24,71$ , median $Q_2=30,32$ , dan kuartil atas $Q_3=34,42$ .

317

3.5 (2 rating)