Tentukan daerah penyelesaian atau himpunan penyelesaian dari SPtLDV berikut dengan cara titik selidik! ⎩ ⎨ ⎧ ​ x + 2 y ≤ 6 2 x − 4 y ≤ 4 x ≥ 1 y ≥ 1 ​

Pembahasan

Daerahpenyelesaian SPtLDV yang diberikan di atas dapat ditentukan dengan prosedur sebagai berikut. Menentukan daerah penyelesaian pertidaksamaan Titik potonggaris lurus dengan sumbu-X dan sumbu-Y padakoordinat kartesius Selanjutnya digambarkan garis lurus melalui kedua titik tersebut. Garis yang terbentuk akan membagi diagram kartesius menjadi dua daerah. Kemudian, pilih salah satu titik uji, di luar garis lurus yang terbentuk, misalnya , kemudian disubstitusikan ke pertidaksamaan asal. Sehingga diperoleh: Karena hasil substitusi menghasilkan pernyataan benar, maka daerah yang memuat titik adalah daerah penyelesaian pertidaksamaan tersebut, seperti yang ditunjukkan pada gambar berikut. 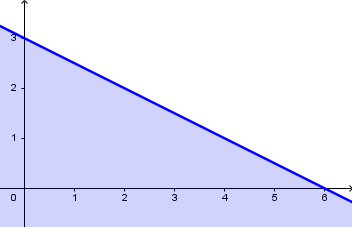Menentukan daerah penyelesaian pertidaksamaan Titik potonggaris lurus dengan sumbu-X dan sumbu-Y padakoordinat kartesius Selanjutnya digambarkan garis lurus melalui kedua titik tersebut. Garis yang terbentuk akan membagi diagram kartesius menjadi dua daerah. Kemudian, pilih salah satu titik uji, di luar garis lurus yang terbentuk, misalnya , kemudian disubstitusikan ke pertidaksamaan asal. Sehingga diperoleh: Karena hasil substitusi menghasilkan pernyataan benar, maka daerah yang memuat titik adalah daerah penyelesaian pertidaksamaan tersebut, seperti yang ditunjukkan pada gambar berikut. 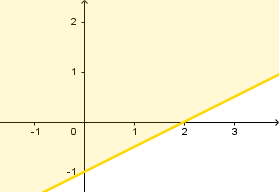Menentukan daerah penyelesaian pertidaksamaan Karena diketahui , maka penyelesaian sistem pertidaksamaan akan berada di kanan garis dan di atas garis , seperti ditunjukkan gambar berikut. 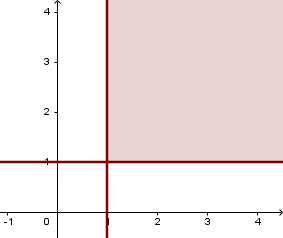Selanjutnya, dapat ditentukan daerah penyelesaian dari SPtLDV yang diberikan yaitu merupakan irisan dari ketiga daerah penyelesaian di atas. Sehingga daerah penyelesaian SPtLDV yang diberikan dapat ditunjukkan oleh daerah yang diarsir pada gambar berikut. 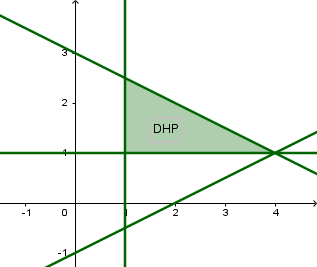Dengan demikian, daerah penyelesaian SPtLDV yang diberikan dapat ditunjukkan oleh gambar di atas.