Susunlah pertidaksamaan linear dua variabel dari daerah penyelesaian berikut!

Pembahasan

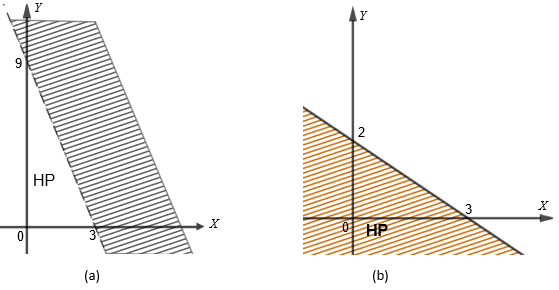
Untuk menentukan pertidaksamaan yang memenuhi daerah penyelesaian yang diberikan pada gambar di atas, dapat dilakukan langkah-langkah berikut. 1. Menentukan persamaan garis lurus pada grafik. Ingat bahwa untuk garis yang memotong sumbu X dan sumbu Y di titik ( x 1 ​ , 0 ) dan ( 0 , y 1 ​ ) maka dapat ditentukan persamaannya dengan rumus berikut. x 1 ​ x ​ + y 1 ​ y ​ = 1 Sehingga untuk gambar (a) dengan titik potong ( 3 , 0 ) dan ( 0 , 9 ) diperoleh: x 1 ​ x ​ + y 1 ​ y ​ 3 x ​ + 9 y ​ 3 x + y ​ = = = ​ 1 1 ( kedua ruas kali 9 ) 9 ​ Untuk gambar (b) dengan titik potong ( 3 , 0 ) dan ( 0 , 2 ) diperoleh: x 1 ​ x ​ + y 1 ​ y ​ 3 x ​ + 2 y ​ 2 x + 3 y ​ = = = ​ 1 1 ( kedua ruas kali 6 ) 6 ​ 2. Menentukan tanda ketaksamaan berdasarkan daerah HP dan jenis garis Pada gambar (a) daerah HP ada di bawah (di kiri) garis. Atau dapat juga dilihat bahwa daerah HP memuat titik (0, 0). Artinya jika titik (0, 0) disubstitusikan ke persamaan maka tanda ketaksamaan yang digunakan dapat membuat hubungan ruas kiri dan kanan menjadi pernyataan yang benar, seperti berikut. 3 x + y 3 ⋅ 0 + 0 0 + 0 0 ​ = = = = ​ 9 ( substitusi titik ( 0 , 0 )) 9 9 9 ​ Agar persamaan di atas menjadi pernyataan benar maka tanda sama dengan diganti dengan tanda ketaksamaan <, sebab 0 < 9 . Karena garisnya putus-putus maka tidak disertai tanda sama dengan pada ketaksamaanya, sehingga diperoleh pertidaksamaan yang memenuhi yaitu 3 x + y < 9 . Pada gambar (b) daerah HP ada di bawah (di kiri) garis. Atau dapat juga dilihat bahwa daerah HP memuat titik (0, 0). Artinya jika titik (0, 0) disubstitusikan ke persamaan maka tanda ketaksamaan yang digunakan dapat membuat hubungan ruas kiri dan kanan menjadi pernyataan yang benar, seperti berikut. 2 x + 3 y 2 ⋅ 0 + 3 ⋅ 0 0 + 0 0 ​ = = = = ​ 6 ( substitusi titik ( 0 , 0 )) 6 6 6 ​ Agar persamaan di atas menjadi pernyataan benar maka tanda sama dengan diganti dengan tanda ketaksamaan <, sebab 0 ​ < ​ 6 ​ . Karena garisnya penuh (tidak putus-putus) maka disertai tanda sama dengan pada ketaksamaanya, sehingga diperoleh pertidaksamaan yang memenuhi yaitu 2 x + 3 y ​ ≤ ​ 6 ​ . Dengan demikian, pertidaksamaan yang memenuhi daerah penyelesaian pada gambar (a) adalah 3 x + y ​ < ​ 9 ​ dan pada gambar (b) adalah 2 x + 3 y ​ ≤ ​ 6 ​ .