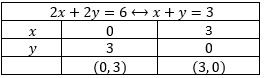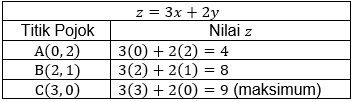Iklan
Iklan
Pertanyaan
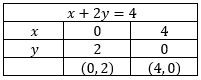
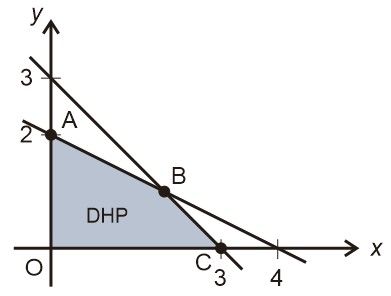
Suatu perusahaan tas dan sepatu memerlukan 4 unsur dan 6 unsur b per minggu untuk masing-masing hasil produksinya. Setiap tas memerlukan 1 unsur dan 2 unsur , setiap sepatu memerlukan 2 unsur dan 2 unsur . Jika setiap tas keuntungannya Rp3.000,00 dan setiap sepatu keuntungannya Rp2.000,00, maka banyak tas dan sepatu yang dihasilkan per minggu agar memperoleh keuntungan maksimaladalah ...
Suatu perusahaan tas dan sepatu memerlukan 4 unsur dan 6 unsur per minggu untuk masing-masing hasil produksinya. Setiap tas memerlukan 1 unsur
dan 2 unsur
, setiap sepatu memerlukan 2 unsur
dan 2 unsur
. Jika setiap tas keuntungannya Rp3.000,00 dan setiap sepatu keuntungannya Rp2.000,00, maka banyak tas dan sepatu yang dihasilkan per minggu agar memperoleh keuntungan maksimal adalah ...
3 tas
4 tas
2 sepatu
3 sepatu
2 tas, 1 sepatu
Iklan
A. Salim
Master Teacher
Mahasiswa/Alumni Universitas Pelita Harapan
49
4.9 (11 rating)
Elly Turnip
Ini yang aku cari!
Iklan
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2024 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia