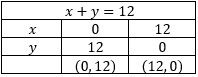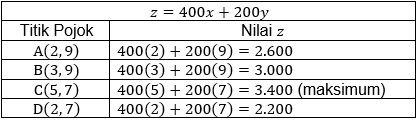Pertanyaan

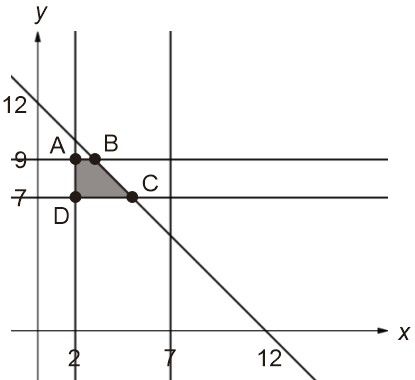
Sebuah pabrik memproduksi barang kualitas A dan B. Produksi maksimum setiap harinya 12 unit. Permintaan konsumen paling sedikit harus dibuat 2 unit barang kualitas A dan 7 unit barang kualitas B. Adapun kemampuan mesin produksi hanya bisa menghasilkan 7 unit barang kualitas A dan 9 unit barang kualitas B. Jika keuntungan dari satu barang kualitas A adalah Rp400,00 dan barang kualitas B Rp200,00. Keuntungan maksimum yang bisa diperoleh adalah ...

Sebuah pabrik memproduksi barang kualitas A dan B. Produksi maksimum setiap harinya 12 unit. Permintaan konsumen paling sedikit harus dibuat 2 unit barang kualitas A dan 7 unit barang kualitas B. Adapun kemampuan mesin produksi hanya bisa menghasilkan 7 unit barang kualitas A dan 9 unit barang kualitas B. Jika keuntungan dari satu barang kualitas A adalah Rp400,00 dan barang kualitas B Rp200,00. Keuntungan maksimum yang bisa diperoleh adalah ... $\;\;$

Rp3.000,00
Rp2.200,00
Rp3.400,00
Rp2.600,00
Rp3.600,00

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Jawaban

jawaban yang benar adalah C.

Pembahasan

Langkah pertama, pertama kita misalkan jumlah barang kualitas A dan jumlah barang kualitas B. Diketahui permintaan konsumen paling sedikit harus dibuat 2 unit barang kualitas A dan 7 unit barang kualitas B. Diketahui pula bahwa kemampuan mesin produksi hanya bisa menghasilkan 7 unit barang kualitas A dan 9 unit barang kualitas B. Maka, diperoleh dua pertidaksamaan, yaitu dan . Langkah kedua adalah membentuk sistem pertidaksamaan dari soal yang diketahui. Diketahui bahwa produksi maksimum setiap harinya 12 unit. Sehingga, diperoleh sistem pertidaksamaan: Langkah ketiga adalah menentukan fungsi tujuan yang akan dioptimumkan. Dari soal tersebut, ditanyakan keuntungan maksimum yang dapat diperoleh. Diketahui keuntungan dari satu barang kualitas A adalah Rp400,00 dan barang kualitas B Rp200,00 sehinggadiperoleh fungsi tujuan . Langkah keempat adalah menggambar daerah himpunan penyelesaian dengan uji titik pada sistem pertidaksamaan yang didapatkan. Setiap persamaan garis dapat digambar dengan mencari titik potong sumbu X dan sumbu Y. Berikut tabel titik potongnya. Grafik beserta daerah himpunan penyelesaiannya adalah: Perhatikan bahwa titik A merupakan titik . Titik Dmerupakan titik . Sedangkan titik pojok B dan C bisa didapatkan dengan substitusi dan eliminasi. Titik B mempunyai ordinat sehingga: Diperoleh titik . Titik Cmempunyai ordinat sehingga: Diperoleh titik . Langkah berikutnya adalah menghitung nilai dari fungsi tujuan dengan uji titik pojok. Berikut tabel uji titik pojoknya. Jadi, keuntungan maksimum yang dapat diperoleh adalah Rp3.400,00. Oleh karena itu, jawaban yang benar adalah C.

Langkah pertama, pertama kita misalkan x equals jumlah barang kualitas A dan y equals jumlah barang kualitas B.

Diketahui permintaan konsumen paling sedikit harus dibuat 2 unit barang kualitas A dan 7 unit barang kualitas B. Diketahui pula bahwa kemampuan mesin produksi hanya bisa menghasilkan 7 unit barang kualitas A dan 9 unit barang kualitas B. Maka, diperoleh dua pertidaksamaan, yaitu 2 less or equal than x less or equal than 7 dan 7 less or equal than y less or equal than 9 .

Langkah kedua adalah membentuk sistem pertidaksamaan dari soal yang diketahui. Diketahui bahwa produksi maksimum setiap harinya 12 unit.

Sehingga, diperoleh sistem pertidaksamaan:

open curly brackets table row cell x plus y less or equal than 12 end cell row cell 2 less or equal than x less or equal than 7 end cell row cell 7 less or equal than x less or equal than 9 end cell end table close

Langkah ketiga adalah menentukan fungsi tujuan yang akan dioptimumkan. Dari soal tersebut, ditanyakan keuntungan maksimum yang dapat diperoleh. Diketahui keuntungan dari satu barang kualitas A adalah Rp400,00 dan barang kualitas B Rp200,00 sehingga diperoleh fungsi tujuan z equals 400 x plus 200 y .

Langkah keempat adalah menggambar daerah himpunan penyelesaian dengan uji titik pada sistem pertidaksamaan yang didapatkan. Setiap persamaan garis dapat digambar dengan mencari titik potong sumbu X dan sumbu Y. Berikut tabel titik potongnya.

Grafik beserta daerah himpunan penyelesaiannya adalah:

Perhatikan bahwa titik A merupakan titik open parentheses 2 comma space 9 close parentheses . Titik D merupakan titik . Sedangkan titik pojok B dan C bisa didapatkan dengan substitusi dan eliminasi.

Titik B mempunyai ordinat y equals 9 sehingga:

table attributes columnalign right center left columnspacing 0px end attributes row cell x plus y end cell equals 12 row cell x plus 9 end cell equals 12 row x equals 3 end table

Diperoleh titik straight B left parenthesis 3 comma space 9 right parenthesis .

Titik C mempunyai ordinat y equals 7 sehingga:

table attributes columnalign right center left columnspacing 0px end attributes row cell x plus y end cell equals 12 row cell x plus 7 end cell equals 12 row x equals 5 end table

Diperoleh titik straight B left parenthesis 5 comma space 7 right parenthesis .

Langkah berikutnya adalah menghitung nilai dari fungsi tujuan dengan uji titik pojok. Berikut tabel uji titik pojoknya.

Jadi, keuntungan maksimum yang dapat diperoleh adalah Rp3.400,00.

Oleh karena itu, jawaban yang benar adalah C.

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

3.8 (6 rating)

Pertanyaan serupa

Sebuah pesawat mempunyai tempat duduk 48 kursi. Penumpang kelas utama boleh membawa bagasi 60 kg, sedangkan kelas ekonomi 20 kg. Harga tiket kelas utama Rp 150.000 , 00 dan kelas ekonomi Rp 100.000 , ...

4.0

Jawaban terverifikasi

Seorang pedagang asongan, membeli barang A dengan harga Rp100,00 dan dapatmenjualnya dengan harga Rp130,00 setiap barangnya. Ia membeli barang B dengan harga Rp200,00 setiap barang dan dapat menjualny...

5.0

Jawaban terverifikasi

Seorang pemilik toko ingin mengisi tokonya dengan sepatu laki-laki paling sedikit 100 pasang dan sepatu wanita paling sedikit 150 pasang. Toko tersebut hanya dapat memuat 400 pasang sepatu. Keuntungan...

4.5

Jawaban terverifikasi

Dengan persediaan kain polos 20 m dan kain bergaris 10 m seorang penjahit akan membuat pakaian. Model I memerlukan 1 m kain polos dan 1,5 m kain bergaris, model II memerlukan 2 m kain polos dan 0,5 m ...

4.5

Jawaban terverifikasi

Seorang pedagang membeli 25 pasang sepatu untuk persediaan. Ia ingin membeli sepatu jenis A dengan harga Rp30.000,00 dan sepatu jenis B seharga Rp40.000,00 . Ia merencanakan tidak akan mengeluarkan ua...

4.6

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS