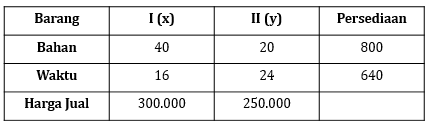
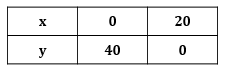
Suatu perusahaan memproduksi dua jenis barang, yaitu barang jenis I dan II. Pembuatan per unit barang jenis I membutuhkan 40 kg bahan mentah dan waktu 16 jam, sedangkan pembuatan per unit barang jenis II membutuhkan 20 kg bahan mentah dan waktu 24 jam. Bahan mentah yang tersedia adalah 800 kg dan lama waktu pembuatan seluruh barang adalah 640 jam. Jika barang jenis I dijual dengan harga Rp 300.000 , 00 per unit dan untuk barang jenis II sebesar Rp 250.000 , 00 per unit, tentukan: a. model matematika dari permasalahan tersebut, b. banyak setiap barang yang harus dijual agar pendapatan yang diperoleh sebesar-besarnya, dan c. pendapatan maksimum yang diperoleh perusahaan tersebut.

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah model matematika 2 x + y ≤ 40 , 2 x + 3 y ≤ 80 , x ≥ 0 , y ≥ 0 , f ( x , y ) = 300 . 000 x + 250 . 000 y . Untuk memperoleh pendapatn maksimum sebesar Rp 8 . 000 . 000 , 00 maka perusahaan harus menjual 10 barang I dan 20 barang II. Program Linear Misalkan barang I ( x ) dan barang II ( y ) maka dapat dibuat tabel berikut: Berdasarkan tabel di atas dapat kita buat model matematika sebagai berikut: a. Model matematika permasalahan di atas Bahan mentah: 40 x + 20 y 2 x + y ​ ≤ ≤ ​ 800 40 ​ Waktu pengerjaan: 16 x + 24 y 2 x + 3 y ​ ≤ ≤ ​ 640 80 ​ Dengan x ≥ 0 , y ≥ 0 . Harga jual merupakan fungsi objektif: f ( x , y ) = 300.000 x + 250.000 y Dengan demikian, model matematika permasalahan di atas adalah 2 x + y ≤ 40 , 2 x + 3 y ≤ 80 , x ≥ 0 , y ≥ 0 , f ( x , y ) = 300.000 x + 250.000 y . b. Menentukan banyak barang yang harus dijual Menentukan titik koordinat grafik 2 x + y ≤ 40 , diperoleh: Diperoleh titik koordinat grafik adalah A ( 0 , 40 ) , B ( 20 , 0 ) . 2 x + 3 y ≤ 80 , diperoleh: Diperoleh titik koordinat grafik adalah C ( 0 , 26 , 67 ) , D ( 40 , 0 ) . Menentukan titik potong grafik 2 x + y ≤ 40 dan 2 x + 3 y ≤ 80 . 2 x 2 x ​ + + ​ y 3 y − 2 y y ​ = = = = ​ 40 80 − 40 20 ​ − ​ ​ Substitusi nilai y = 20 ke: 2 x + y 2 x + 20 2 x 2 x x ​ = = = = = ​ 40 40 40 − 20 20 10 ​ Diperoleh titik potong grafik adalah E ( 10 , 20 ) . Berikut gambar daerah penyelesaiannya: Daerah penyelesaian grafik fungsi di atas di batasi oleh titik O ( 0 , 0 ) , B ( 20 , 0 ) , E ( 10 , 20 ) , dan C ( 0 , 26 , 67 ) . 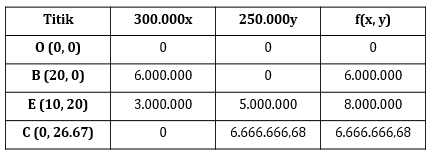Melakukan uji titik pojok: Berdasarkan hasil uji titik pojok di atas dapat kita simpulkan bahwa banyaksetiap barang yang harus dijual agar pendapatan yang diperoleh sebesar-besarnya adalah 10 barang I dan 20 barang II. Dengan demikian, barang yang harus dijual sebanyak 10 barang I dan 20 barang II. c. Pendapatan maksimum yang diperoleh perusahaan Berdasarkan tabel uji titik pojok di atas diperoleh pendapatan maksimum yang diperoleh adalah sebesar Rp 8.000.000 , 00 . Dengan demikian, pendapatan maksimumnya adalah Rp 8.000.000 , 00 .

Yah, akses pembahasan gratismu habis

Tonton iklanTonton iklanAkses jawaban tanpa iklan

---

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang