Pertanyaan

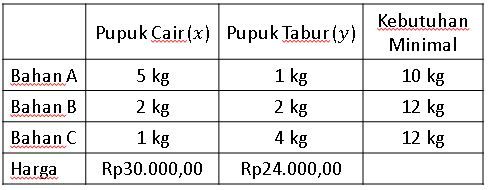
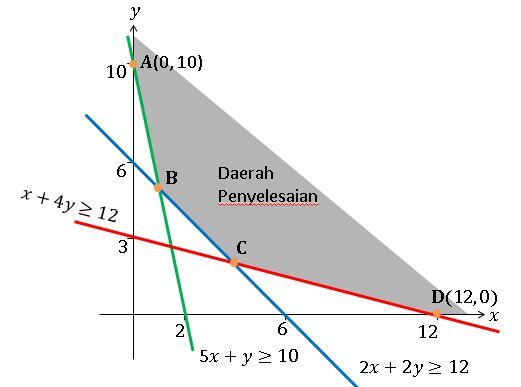
Seorang petani memerlukan sedikitnya 10 kg bahan organik A, 12 kg bahan organik B, dan 12 kg bahan organik C untuk menyuburkan tanamannya. Kebutuhan itu dipenuhi dari pupuk cair yang mengandung 5 kg A, 2 kg B, dan 1 kg C tiap botol dan pupuk tabur yang mengandung 1 kg A, 2 kg B, dan 4 kg C tiap kantong. Harga pupuk cair Rp 30.000 , 00 per botol dan pupuk tabur Rp 24.000 , 00 per kantong. Banyaknya setiap jenis pupuk harus dibeli agar biaya pemupukan seminimal mungkin adalah ....

Seorang petani memerlukan sedikitnya $10 kg$ bahan organik A, $12 kg$ bahan organik B, dan $12 kg$ bahan organik C untuk menyuburkan tanamannya. Kebutuhan itu dipenuhi dari pupuk cair yang mengandung $5 kg$ A, $2 kg$ B, dan $1 kg$ C tiap botol dan pupuk tabur yang mengandung $1 kg$ A, $2 kg$ B, dan $4 kg$ C tiap kantong. Harga pupuk cair $Rp 30.000, 00$ per botol dan pupuk tabur $Rp 24.000, 00$ per kantong. Banyaknya setiap jenis pupuk harus dibeli agar biaya pemupukan seminimal mungkin adalah ....

$2 kg$ pupuk cair, $0 kg$ pupuk tabur
$0 kg$ pupuk cair, $3 kg$ pupuk tabur
$0 kg$ pupuk cair, $2 kg$ pupuk tabur
$1 kg$ pupuk cair, $5 kg$ pupuk tabur
$2 kg$ pupuk cair, $3 kg$ pupuk tabur

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

D. Rajib

Master Teacher

Mahasiswa/Alumni Universitas Muhammadiyah Malang

Jawaban terverifikasi

Jawaban

jawaban yang benar adalah D.

Pembahasan

Soal cerita di atas merupakan permasalahan program linear. Misalkan: x y = = banyak botol pupuk cair banyak kantong pupuk tabur Dari permasalahan tersebut, dapat disederhanakan dalam bentuk tabel sebagai berikut. Sehingga diperoleh model matematika sistem pertidaksamaan untuk fungsi kendala sebagai berikut: { 5 x + y ≥ 10 2 x + 2 x ≥ 12 x + 4 y ≥ 12 x ≥ 0 y ≥ 0 Sedangkan fungsi tujuannya, yaitu: F ( x , y ) = 30.000 x + 24.000 y Mencari titik potong pertidaksamaan terhadap sumbu x dan sumbu y . Untuk 5 x + y ≥ 10 , titik potongnya yaitu: x = 0 y = 0 → → 5 ( 0 ) + y = 10 y = 10 5 x + 0 = 10 x = 5 10 = 2 → → ( 0 , 10 ) ( 2 , 0 ) Untuk 2 x + 2 y ≥ 12 , titik potongnya yaitu: x = 0 y = 0 → → 2 ( 0 ) + 2 y = 12 y = 2 12 = 6 2 x + 2 ( 0 ) = 12 x = 2 12 = 6 → → ( 0 , 6 ) ( 6 , 0 ) Untuk x + 4 y ≥ 12 , titik potongnya yaitu: x = 0 y = 0 → → ( 0 ) + 4 y = 12 y = 4 12 = 3 x + 4 ( 0 ) = 12 x = 12 → → ( 0 , 3 ) ( 12 , 0 ) Grafik daerah penyelesaian dari sistem pertidaksamaan tersebut, yaitu: Titik A, B, C dan titik D merupakan titik pojok pada daerah penyelesaian dari sistem pertidaksamaaan fungsi kendala. Titik B dan titik C dapat diperoleh dengan menggunakan metode eliminasi-substitusi. Mencari titik B: Eliminasi persamaan garis 5 x + y = 10 dan persamaan garis 2 x + 2 y = 12 . 5 x + y = 10 2 x + 2 y = 12 ∣ × 2∣ ∣ × 1∣ 10 x + 2 y = 20 2 x + 2 y = 12 8 x = 8 x = 8 8 = 1 − Substitusi x = 1 ke persamaan 2 x + 2 y = 12 . 2 x + 2 y 2 ( 1 ) + 2 y 2 y y = = = = = 12 12 12 − 2 2 10 5 Sehingga diperoleh titik B ( 1 , 5 ) . Mencari titik C: Eliminasi persamaan garis x + 4 y = 12 dan persamaan garis 2 x + 2 y = 12 . x + 4 y = 12 2 x + 2 y = 12 ∣ × 2∣ ∣ × 1∣ 2 x + 8 y = 24 2 x + 2 y = 12 6 y = 12 y = 6 12 = 2 − Substitusi y = 2 ke persamaan 2 x + 2 y = 12 . 2 x + 2 y 2 x + 2 ( 2 ) 2 x x = = = = = 12 12 12 − 4 2 8 4 Sehingga diperoleh titik C ( 4 , 2 ) . Mencari biaya minimal dapat digunakan metode titik pojok sebagai berikut: Substitusi masing-masing titik pojok ke fungsi tujuan. Titik A ( 0 , 10 ) : F ( 0 , 10 ) = = 30.000 ( 0 ) + 24.000 ( 10 ) 240.000 Titik B ( 1 , 5 ) : F ( 1 , 5 ) = = 30.000 ( 1 ) + 24.000 ( 5 ) 150.000 Titik C ( 4 , 4 ) : F ( 4 , 4 ) = = 30.000 ( 4 ) + 24.000 ( 4 ) 216.000 Titik D ( 12 , 0 ) : F ( 12 , 0 ) = = 30.000 ( 12 ) + 24.000 ( 0 ) 360.000 Berdasarkan perhitungan tersebut, titik B ( 1 , 5 ) memberikan biaya paling minimum yaitu Rp150.000. Dengan demikian,Banyaknya setiap jenis pupuk harus dibeli agar biaya pemupukan seminimal mungkin adalah 1 botol pupuk cair dan 5 kantong pupuk tabur. Keterangan : Pada pilihan jawabantertulis satuan kilogram untuk setiap jenis pupuk.Seharusnya satuan banyak pupuk cair adalah botol, dan satuan banyak pupuk tabur adalah kantong. Oleh karena itu, jawaban yang benar adalah D.

Soal cerita di atas merupakan permasalahan program linear.

Misalkan:

$x y = = banyak botol pupuk cair banyak kantong pupuk tabur$

Dari permasalahan tersebut, dapat disederhanakan dalam bentuk tabel sebagai berikut.

Sehingga diperoleh model matematika sistem pertidaksamaan untuk fungsi kendala sebagai berikut:

${5 x + y \geq 102 x + 2 x \geq 12 x + 4 y \geq 12 x \geq 0 y \geq 0$

Sedangkan fungsi tujuannya, yaitu:

$F (x, y) = 30.000 x + 24.000 y$

Mencari titik potong pertidaksamaan terhadap sumbu $x$ dan sumbu $y$ .

Untuk $5 x + y \geq 10$ , titik potongnya yaitu:

$x = 0 y = 0 \to \to 5 (0) + y = 10 y = 10 5 x + 0 = 10 x = \frac{10}{5} = 2 \to \to (0, 10) (2, 0)$

Untuk $2 x + 2 y \geq 12$ , titik potongnya yaitu:

$x = 0 y = 0 \to \to 2 (0) + 2 y = 12 y = \frac{12}{2} = 6 2 x + 2 (0) = 12 x = \frac{12}{2} = 6 \to \to (0, 6) (6, 0)$

Untuk $x + 4 y \geq 12$ , titik potongnya yaitu:

$x = 0 y = 0 \to \to (0) + 4 y = 12 y = \frac{12}{4} = 3 x + 4 (0) = 12 x = 12 \to \to (0, 3) (12, 0)$

Grafik daerah penyelesaian dari sistem pertidaksamaan tersebut, yaitu:

Titik A, B, C dan titik D merupakan titik pojok pada daerah penyelesaian dari sistem pertidaksamaaan fungsi kendala. Titik B dan titik C dapat diperoleh dengan menggunakan metode eliminasi-substitusi.

Mencari titik B:

Eliminasi persamaan garis $5 x + y = 10$ dan persamaan garis $2 x + 2 y = 12$ .

$5 x + y = 10 2 x + 2 y = 12 ∣ \times 2∣ ∣ \times 1∣ 10 x + 2 y = 20 2 x + 2 y = 12 8 x = 8 x = \frac{8}{8} = 1 -$

Substitusi $x = 1$ ke persamaan $2 x + 2 y = 12$ .

$2 x + 2 y 2 (1) + 2 y 2 y y = = = = = 1212 12 - 2 \frac{10}{2} 5$

Sehingga diperoleh titik $B (1, 5)$ .

Mencari titik C:

Eliminasi persamaan garis $x + 4 y = 12$ dan persamaan garis $2 x + 2 y = 12$ .

$x + 4 y = 12 2 x + 2 y = 12 ∣ \times 2∣ ∣ \times 1∣ 2 x + 8 y = 24 2 x + 2 y = 12 6 y = 12 y = \frac{12}{6} = 2 -$

Substitusi $y = 2$ ke persamaan $2 x + 2 y = 12$ .

$2 x + 2 y 2 x + 2 (2) 2 x x = = = = = 1212 12 - 4 \frac{8}{2} 4$

Sehingga diperoleh titik $C (4, 2)$ .

Mencari biaya minimal dapat digunakan metode titik pojok sebagai berikut:

Substitusi masing-masing titik pojok ke fungsi tujuan.

Titik $A (0, 10)$ :

$F (0, 10) = = 30.000 (0) + 24.000 (10) 240.000$

Titik $B (1, 5)$ :

$F (1, 5) = = 30.000 (1) + 24.000 (5) 150.000$

Titik $C (4, 4)$ :

$F (4, 4) = = 30.000 (4) + 24.000 (4) 216.000$

Titik $D (12, 0)$ :

$F (12, 0) = = 30.000 (12) + 24.000 (0) 360.000$

Berdasarkan perhitungan tersebut, titik $B (1, 5)$ memberikan biaya paling minimum yaitu Rp150.000.

Dengan demikian, Banyaknya setiap jenis pupuk harus dibeli agar biaya pemupukan seminimal mungkin adalah 1 botol pupuk cair dan 5 kantong pupuk tabur.

Keterangan: Pada pilihan jawaban tertulis satuan kilogram untuk setiap jenis pupuk. Seharusnya satuan banyak pupuk cair adalah botol, dan satuan banyak pupuk tabur adalah kantong.

Oleh karena itu, jawaban yang benar adalah D.

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.6 (3 rating)

Sabrina Salsabila Despran

Pembahasan lengkap banget Ini yang aku cari! Bantu banget Makasih ❤️

Qorina Maya S

Ini yang aku cari!

Pertanyaan serupa

Sebuah pesawat mempunyai tempat duduk 48 kursi. Penumpang kelas utama boleh membawa bagasi 60 kg, sedangkan kelas ekonomi 20 kg. Harga tiket kelas utama Rp 150.000 , 00 dan kelas ekonomi Rp 100.000 , ...

4.0

Jawaban terverifikasi

Seorang pedagang asongan, membeli barang A dengan harga Rp100,00 dan dapatmenjualnya dengan harga Rp130,00 setiap barangnya. Ia membeli barang B dengan harga Rp200,00 setiap barang dan dapat menjualny...

5.0

Jawaban terverifikasi

Seorang pemilik toko ingin mengisi tokonya dengan sepatu laki-laki paling sedikit 100 pasang dan sepatu wanita paling sedikit 150 pasang. Toko tersebut hanya dapat memuat 400 pasang sepatu. Keuntungan...

4.5

Jawaban terverifikasi

Tanah seluas 10.000 m 2 akan dibangun rumah tipe A dan tipe B. Untuk tipe Bdiperlukan 100 m 2 dan tipe B diperlukan 75 m 2 .Jumlah rumah yang akan dibangunpaling banyak 125 unit. Keuntungan rumah tipe...

4.3

Jawaban terverifikasi

Dengan persediaan kain polos 20 m dan kain bergaris 10 m seorang penjahit akan membuat pakaian. Model I memerlukan 1 m kain polos dan 1,5 m kain bergaris, model II memerlukan 2 m kain polos dan 0,5 m ...

4.5

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS