Iklan
Pertanyaan
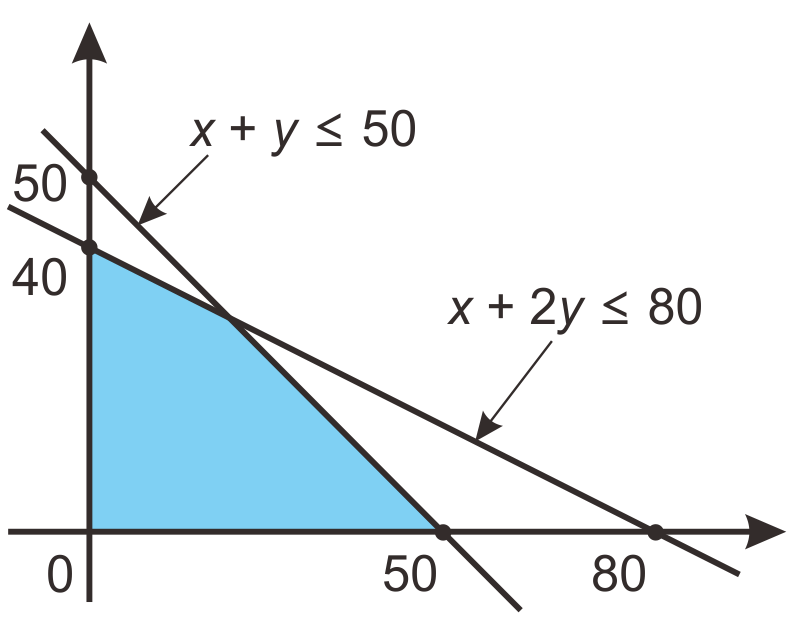
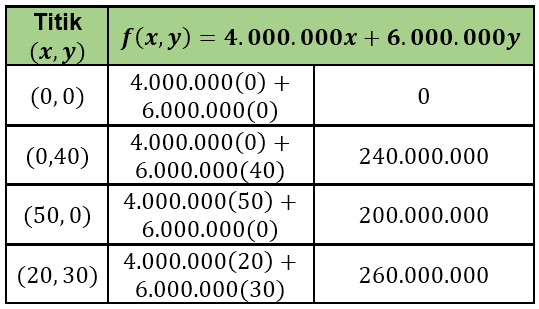
Seorang petani akan menanam jagung dan singkong dengan lahan yang dibutuhkan tidak lebih dari 50 petak. Petani tersebut membutuhkan pupuk sebanyak 30 kg per petak untuk memupuk jagung dan 60 kg per petak untuk memupuk singkong. Jumlah pupuk yang tersedia 2.400 kg. Jika keuntungan lahan jagung adalah Rp4.000.000,00 per petak dan lahan singkong adalah Rp6.000.000,00 per petak dalam sekali tanam, keuntungan maksimum petani tersebut adalah ....
Seorang petani akan menanam jagung dan singkong dengan lahan yang dibutuhkan tidak lebih dari 50 petak. Petani tersebut membutuhkan pupuk sebanyak 30 kg per petak untuk memupuk jagung dan 60 kg per petak untuk memupuk singkong. Jumlah pupuk yang tersedia 2.400 kg. Jika keuntungan lahan jagung adalah Rp4.000.000,00 per petak dan lahan singkong adalah Rp6.000.000,00 per petak dalam sekali tanam, keuntungan maksimum petani tersebut adalah ....
Rp460.000.000,00
Rp360.000.000,00
Rp325.000.000,00
Rp260.000.000,00
Rp160.000.000,00
Iklan
D. Kamilia
Master Teacher
Mahasiswa/Alumni Universitas Negeri Malang
16
4.5 (22 rating)
Khoirunnisa fs
Mudah dimengerti Ini yang aku cari!
Ismail Febrianto
Soal tidak sesuai
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia