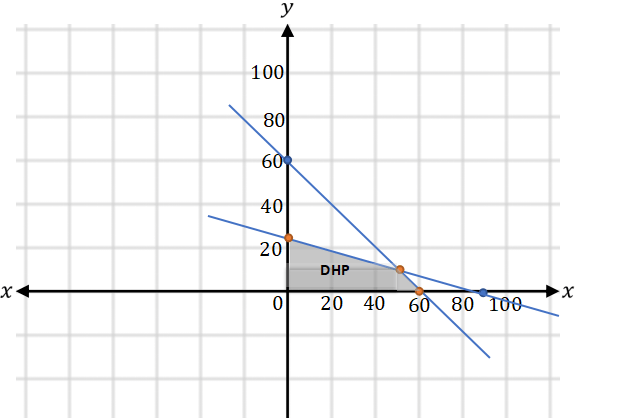
Luas daerah parkir sebuah tempat wisata 540 m 2 . Luas rata-rata untuk sebuah mobil 6 m 2 dan sebuah bus 24 m 2 . Daerah perkir tersebut tidak dapat memuat lebih dari 60 kendaraan. Peraturan biaya parkir tersebut adalah : Mobil Rp2.000,00 dan bus Rp6.000,00 Bagaimana menghitung banyak mobil dan bus agar parkir memperoleh pendapatan maksimal?

Pembahasan

Misalkan x dan y berturut-turut menyatakan banyaknya mobil dan bus yang parkir. Maka, Selanjutnya gambarkan daerah penyelesaian dari sitem pertidaksamaan tersebut. Pertama tentukan titik potong garis dengan sumbu-sumbu koordinat: x + y = 60 → ( 0 , 60 ) ( 60 , 0 ) x + 4 y = 90 → ( 0 , 2 45 ​ ) ( 90 , 0 ) Untuk koefisien x positif, jika simbol pertidaksamaan adalah ≤ , maka daerah penyelesaian adalah di sebelah kiri garis. Perhatikan gambar berikut: Selanjutnya, tentukan titik potong garis : x + y = 60 x + 4 y = 90 − ​ ​ − 3 y = − 30 y = 10 x + 10 = 60 x = 50 ( x , y ) = ( 50 , 10 ) ​ Diperoleh titik pojoh DHP yaitu ( 0 , 2 45 ​ ) , ( 60 , 0 ) , dan ( 50 , 10 ) . Uji titik pojok daerah ke fungsi objektif : f ( 0 , 2 45 ​ ) f ( 60 , 0 ) f ( 50 , 10 ) ​ = = = = = = = = ​ 2.000 ( 0 ) + 6.000 ( 2 45 ​ ) 3.000 ( 45 ) 135.000 2.000 ( 60 ) + 6.000 ( 0 ) 120.000 2.000 ( 50 ) + 6.000 ( 10 ) 100.000 + 60.000 160.000 ( maks ) ​ Jadi, diperoleh pendapatan maksimal tukang parkir tersebut ketika jumlah mobil dan bus yang parkir berturut-turut 50 mobil dan 10 bus, dengan pendapatan maksimalnya adalah Rp160.000.

Yah, akses pembahasan gratismu habis

Tonton iklanTonton iklanAkses jawaban tanpa iklan

---

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang