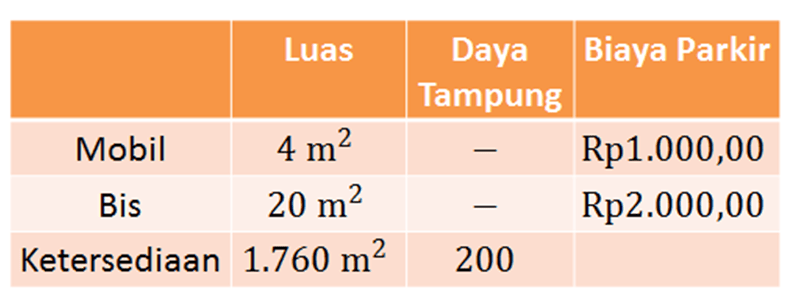
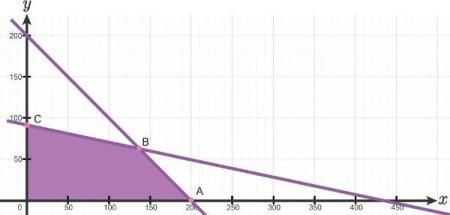
Sebuah waterpark memiliki tempat parkir dengan luas 1.760 meter persegi. Untuk memarkirkan mobil rata-rata memerlukan luas 4 meter persegi, sedangkan untuk bis memerlukan luas 20 meter persegi. Sementara daya tamping tempat parkir hanya 200 kendaraan. Untuk biaya parkir mobil Rp 1.000 , 00 dan bis Rp 2.000 , 00 . Maka keuntungan maksimum tempat parkir tersebut adalah ....

Pembahasan

Menentukan sistem pertidaksamaan linearnyayaitu: Misalkan: x : Banyakm obi l y : Banyak bus Dari soal yang diberikan, dapat diubah ke bentuk tabel sebagai berikut: sistem pertidaksamaan linearpertama berdasarkan luas lahandidapat: sistem pertidaksamaan linear kedua berdasarkan daya tampung didapat : x + y ≤ 200 ... ( 2 ) sistem pertidaksamaan linear ketiga adalah karena banyak mobil dan banyak bus tidak mungkin negatif. Fungsi Tujuan/Objektif (Biaya Parkir) Menentukan titik potong terhadap sumbu dan sumbu untuk setiap pertidaksamaan. x + 5 y = 440 Titik potong terhadap sumbu , dengan substitusi . 0 + 5 y 5 y y y ​ = = = = ​ 440 440 5 440 ​ 88 ​ Titik potong terhadap sumbu , dengan substitusi . x + 5 ( 0 ) x ​ = = ​ 440 440 ​ diperoleh titik potong dari persamaan x + 5 y = 440 adalah ( 0 , 88 ) dan ( 440 , 0 ) . x + y = 200 ​​​​​​​ Titik potong terhadap sumbu , dengan substitusi . 0 + y y ​ = = ​ 200 200 ​ Titik potong terhadap sumbu , dengan substitusi . x + 0 x ​ = = ​ 200 200 ​ diperoleh titik potong dari persamaan x + y = 200 adalah ( 0 , 200 ) dan ( 200 , 0 ) . Selanjutnya, gambarkan daerah himpunan penyelesaiannya . Ingat : 0makaberlaku end text a x plus b y greater or equal than c space rightwards double arrow space text daerahpenyelesaiandikanangaris end text a x plus b y less or equal than c space rightwards double arrow space text daerahpenyelesaiandikirigaris end text" data-mathml="«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mtext»Jika§#160;a§#62;0§#160;maka§#160;berlaku§#160;«/mtext»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi»a«/mi»«mi»x«/mi»«mo»+«/mo»«mi»b«/mi»«mi»y«/mi»«mo»§#8805;«/mo»«mi»c«/mi»«mo»§#160;«/mo»«mo»§#8658;«/mo»«mo»§#160;«/mo»«mtext»daerah§#160;penyelesaian§#160;di§#160;kanan§#160;garis«/mtext»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi»a«/mi»«mi»x«/mi»«mo»+«/mo»«mi»b«/mi»«mi»y«/mi»«mo»§#8804;«/mo»«mi»c«/mi»«mo»§#160;«/mo»«mo»§#8658;«/mo»«mo»§#160;«/mo»«mtext»daerah§#160;penyelesaian§#160;di§#160;kiri§#160;garis«/mtext»«/math»" role="math" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAVYAAABcCAYAAAA1Q51RAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAABGJhU0UAAAAva/WvxwAADSZJREFUeNrtmwFkVt0fx6/HvCaPkcnMZCRJksjMJIlkkszIzCQzkiRJJHm98nqZV5JX4pUkmZEkySuSJHmN1yTJxCRJEskkM+P+f7/6Pv6n27n3nnOfc5+nte+Hr+259+yc3/mdc373d859FkWEEEIIIYQQQgghhBBCCCGEEEIIWR7EKb/bPjeCh6KtHuW17LRoQfREtK3JPvwR66un7phLhJCwC60Zi6pPdN8xwK4RzYi24LP+fIHrDKwMrIQwsGYE2L6UMhdEY4lro7jOwMrASsgPfxSwW3RH1GJc2yuawjb8tWgkpy3f8maAfWAJsLOiVYlr7aJXOf1dj/o+i56JDosOiJ6K5mHboIfdof2k9e1C/z6KhlPKDaM+PQrptNRROyZZzBjjevsWMxgTUiyw6gJ+JKom7k+INuD3bQgCWfiWNzlusW8xpexCTn+viHrxuQfXbuFaBUcK7z3sDu0nrW9StBr2nLcciwzgut4/hD4l67iLh0hW0Ku3bwyshBQIrEdEz5EJNmOb2Yfs0paxpgXWec82fYND2X5K3m9D1m7yFIE3QnC1BcT2AG3n9Y2BlZACgfW06LElU1G6RVdFcwhyeQvKp3wtoD6K0s9YX1iOAlZhCx0ysObZHdpPscPDYh7lalp0DG6xp215fWNgJaTgUcDB6OtLpNbEfT2fPCFa4bigXMqbATXvq1P6kmo0cU0/XwwcWPPsDu2n5P2u6OtZqck9UUeBrDj2tC2vb8ny6xlYCXF/eTUUfT2zMxfWJ9EmbEX3oHzWYncp7xJQa9S+brUZn3uRra4JHFjz7A7tJ70/LlqJevQcdGeizHbRDUvG7htY6+3bWzwM9e/3IVAzsJJlTQULyyWwKv2im9H/3wrrG+QPkG4Xz4neZbTnW94FDcL6jwELyOrygnKRwJpnd2g/zSFI6bmmfsNhR0q5ASOQuf5zR+w5Jnl92wMbFxB01zKwkuXOKLIhQgghdaIZkX6H807GVpIQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBClhWxY7lB0USA9vpFf4ralpn/losdS7lf8Q/Sx3iZjvVPNf9dDfpNdDJQm4dFM/jZLA4ysHLBLNE+MrAGokN0WzQveifqa8KgXhcNBGy3DZnrU9GOJvj0rGhS9AsDKwMrA+vyY4XouWgIn0+J9ifK3EoE25Wie6LOgIP0QrRX9J9oQXQicf8V2k3yr2hDRr1r8dC4I1qXY0OX6KJoTvSHxyTM0qMUu9MYE82Knon2WfynPpqCj16LRix1DOPetGWMtL6tuLfoUW8M/+m4fxa9FO128M0u9OeN6GhKuTx709qtou5K4m9aMF/aHOv3sWcQ9xYLjE2R8r4+d5lDPkcBu7F2WgLbXVbfR9F3TRCPFPS5bX3EHvPgC8eRXdW4ZMkcuxDwKsjAbiBgFQk0NiMqMPCyaDU+a4DbbJS5hs4kJ9BZx4D1KyZIGjvRRhcW7KVAD67JnHZNdCLoOXMrgvG4xV8TxoNkm+hj4r6O3Xn48JDoimV87orWe9YbY6EOoO5eBMu8BTppjOl5LHRfe7PavWBJBEYxf1zr97FHH7rdKf118WHZPneZQ66BdRiJQbUEu8vq+z94oGrCeKagz23rI/aYB194gAZqaKU9lnInoSuJgBciY+3FAJrsSWSNQ8ZiUdrh+GpO3bWM9XbGw2Al6motuM3K0kOPjHUGQahodhHh6GO18cCyTZz2AuMWW/zna1sb/OFrb1a767FrMZk2FoZL/T72zGAdtBb0Ydk+d5lDLnYcwU62WXOlSB0vHAKiS7vtDuVy58FHYytVQdpdsZRbg6xyewnnNfpkvGq59rfxuROT3sysRwKdsQ5Z2g9xxnrd84x1wcF/3bB1LmUbMp8I7IuO45FXb1xgbG33PwSwN3lNt4tb8HsfkoWi9eeV14X7WPQ2+voNlHp8WIbPFxyDR964nUY/qyXNlWb1vUi7tutZ8+ALT4yo22uZ+MoqVDKE9Dp0YP0L2y6T29H3L9Fmkf31WDJck8N42h5xtHG/ZctXL2MF/mY6+vZrYqst/nuG8+cVGUGmo8B45NUbIrB24binXnuT13Yb9U7gHK1o/XnlzTbf1unDMnzuModcx+0gdhitJdhdRt+nEg+CSqB2s67b5sEXzuD8sYIA9y5xv4rJttHIFHsCB9abovvGWdzRyP7y6ArOWaej9BdWte+x+rww6oTDN6H94SjsNyNcOYAxqKB/0xb/fTLs3IP7ZiDQHcUNPAx9xiOv3qKBdRxjoYvzmmXcithru/YcR1SzddafV77GRsuC8vVhGT53mUM+D8QhHA+2Bra7rL7Xzse7sWMM0W7W9Y1pgVXf9p3CYGzAedUw7uk2Vl+8bE2cbU4VPI9MQ4P5LmTPrzK2+DrI7yP3F1Y+dCDAq5OORc1jBD6YxUMittz/AOl27ZzlYTiAB0Xssajy6i0aWMfQHz2S2ZlSztde27VjaOdkgPrzysdoq79OH5bhc5c55LvT6MfaaAlod1l9192qvq1/Cbs/B2g38pwHUVqgrUQ/Jhr430TZL6z6cU5m062INJJGfh+yijO2NrqdGMzQBflcNbJpwsBqYn7FiixP9L2MeUyp705+p1uy0Uz0Pt2wpJhvYFvPoux/FCE/P/od6aeYd3ocMB59+48NhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCFOxI7lBkUTJdqxQ/TnT+y/5WLHUu5X/IP0Ma7TzngJzJmfdb56d/A30ckS2l8rug2ta2C/DzKwMrAu0T4uB580hA4EnnnRO1FfEwb1umggYLttyFCfinY2wadnRZOiXxhYGVgZWJcfK0TPRUP4fEq0P1HmViLYrhTdE3UGHKQXor2i/0QLohOJ+6/QbpJ/RRsS1w6jT0dEFQ9fdIkuiuZEf3hMwiw9SrE7jTHRrOiZaJ/Ff+qjKfjotWjEUscw7k1bxkjr24p7ix71xsj4ddw/i16Kdjv4Zhf680Z0NKVcnr1p7VZRd3KMWzBf2hzr97FnEPcWC4xNkfK+PneZQz5bfW3vDnyadbRgm1Mua38Utr7Dei3iI5e2s8atFI4ju6pxyZI5diHgVZCB3cAWu0igsXWqgg5fFq3GZw1wm40y1+Cc5AQ6m7i2G4uq29MPO9FGFxbspUD+ncTEdEEnlp4ztyIYj1v8NWE8SLaJPibu69idhw8Pia5YxueuaL1nvTEW6gDq7kWwzFugk8aYnsdC97U3q90LlkRgFPPHtX4fe+Yy5paLD8v2ucsccg2sw0gMqjl/nzanYgdb/8EDUBO8MwV95NL2XIGYUBcPYHANNbLHUu4kdCUR8EJkrL0YQJM9iaxxyFgsSjsmXdVSn2asM/jpwkrU1Vpwm5Wlhx4Z6wyCUNHsIsLRx2rjgWWbiO0Fxi22PEx9bWuDP3ztzWp3PXYtJtPGQnOp38eeGayD1oI+LNvnLnPIxY4j2PW1O9rZXmDtvygQjIu27TNuQfhobKUq2HLYts9rkFVuL+G8Rp+MVy3X/jY+d2LSm5n1SEad5hnrjpz2hyzt14tm0tcjvzPWBQf/dcPWuZRtzXwisC86jkdevXGBsbXd/xDA3uQ13Spvwe99SBaK1p9XXgPBY9FbUX+dPizD5wuOwShv3E6jn9U66osbMN9d284at1J4YkTxXsvEV1bBqCGk66ED61/Ydpncjr5/iTaL7K/HkuGmsQ513cLDwcZ+y5avXsYK/M20cS4YIfNI+k8z6xPYOqUFmY4C45FXb4jA2oXjnnrtjS3HP5eNrePeOurPK2+2+bZOH5bhc5c55DpuB7HDaC0psE4lAnclkI+yrtvGrRQ0UP6KTmmAe5e4X8Vk22hkij2BA+tN0X3jLO5oZH95pMFvEJNng2c/d0bpL6Q6MYCb0P5wFPabEa4cwBhU0L9pi/8+GXbuwX0zEOiO4gYehj7jkVdv0cA6joehLs5rlnErYq/t2nMcUc3WWX9e+RobLQvU14dl+NxlDvk8EIdwPNhaQmBVW2vn2d3Y4YXwUdb1jY0KrPq27xQGYwPOq4ZxT7ex+uJla+JscyrwWYUG813Inl9lbPF1kN9H37+wCkEHArw6/VjUPEbgg1lsWWLL/Q+QbtfOWR6GA3hQxB6LIK/eooF1DP3J+tqbr722a8fQzskA9eeVj9FWf50+LMPnLnPId6fRj7XREjiwKvoeRN/Wv0Q7nwP4KPIct4bQEvl9RamRaOB/k3LuY06C+RTdikgjaeT3Ias4s2uj25c0M3RB47lqZNOEgdXE/IoVWRrouw/zWFHfdfxOtzQWzUTv0w1LivkGtvUs8j93J81Fv9P8FPNEjwPGo2//EWHJ8T84zeMtzCk2KgAAAnB0RVh0TWF0aE1MADxtYXRoIHhtbG5zPSJodHRwOi8vd3d3LnczLm9yZy8xOTk4L01hdGgvTWF0aE1MIj48bXRleHQ+SmlrYSYjeEEwO2EmZ3Q7MCYjeEEwO21ha2EmI3hBMDtiZXJsYWt1JiN4QTA7PC9tdGV4dD48bXNwYWNlIGxpbmVicmVhaz0ibmV3bGluZSIvPjxtc3BhY2UgbGluZWJyZWFrPSJuZXdsaW5lIi8+PG1pPmE8L21pPjxtaT54PC9taT48bW8+KzwvbW8+PG1pPmI8L21pPjxtaT55PC9taT48bW8+JiN4MjI2NTs8L21vPjxtaT5jPC9taT48bW8+JiN4QTA7PC9tbz48bW8+JiN4MjFEMjs8L21vPjxtbz4mI3hBMDs8L21vPjxtdGV4dD5kYWVyYWgmI3hBMDtwZW55ZWxlc2FpYW4mI3hBMDtkaSYjeEEwO2thbmFuJiN4QTA7Z2FyaXM8L210ZXh0Pjxtc3BhY2UgbGluZWJyZWFrPSJuZXdsaW5lIi8+PG1zcGFjZSBsaW5lYnJlYWs9Im5ld2xpbmUiLz48bWk+YTwvbWk+PG1pPng8L21pPjxtbz4rPC9tbz48bWk+YjwvbWk+PG1pPnk8L21pPjxtbz4mI3gyMjY0OzwvbW8+PG1pPmM8L21pPjxtbz4mI3hBMDs8L21vPjxtbz4mI3gyMUQyOzwvbW8+PG1vPiYjeEEwOzwvbW8+PG10ZXh0PmRhZXJhaCYjeEEwO3BlbnllbGVzYWlhbiYjeEEwO2RpJiN4QTA7a2lyaSYjeEEwO2dhcmlzPC9tdGV4dD48L21hdGg+2YR5JwAAAABJRU5ErkJggg=="> Daerah himpunan penyelesaian atau arsirannya ke kanandari sumbu . Daerah himpunan penyelesaian atau arsirannya ke atasdari sumbu . Menentukan titik potong Pertidaksamaan (1) dan (2) dengan cara: - Eliminasi (1) dan (2) - Substitusi nilai ke (2) Dari pertidaksamaan (1) dan (2) dapat dibuat daerah penyelesaiannya seperti gambar berikut: Dari gambar di atas, didapat titik - titik pojok yang membatasi daerah penyelesaiannya adalah : ( 0 , 0 ) ; ( 200 , 0 ) ; ( 140 , 60 ) ; ( 0 , 88 ) substitusikan titik - titik pojoknya ke fungsi objektifnya didapat sebagai berikut: f ( x , y ) ( 0 , 0 ) ( 200 , 0 ) ( 140 , 60 ) ( 0 , 88 ) ​ = = = = = = = = = = ​ 1.000 x + 2.000 y 1.000 ( 0 ) + 2.000 ( 0 ) 0 1.000 ( 200 ) + 2.000 ( 0 ) 200.000 1.000 ( 140 ) + 2.000 ( 60 ) 140.000 + 120.000 260.000 1.000 ( 0 ) + 2.000 ( 88 ) 176.000 ​ Jadi,keuntungan maksimum tempat parkir tersebut adalah .