Pertanyaan

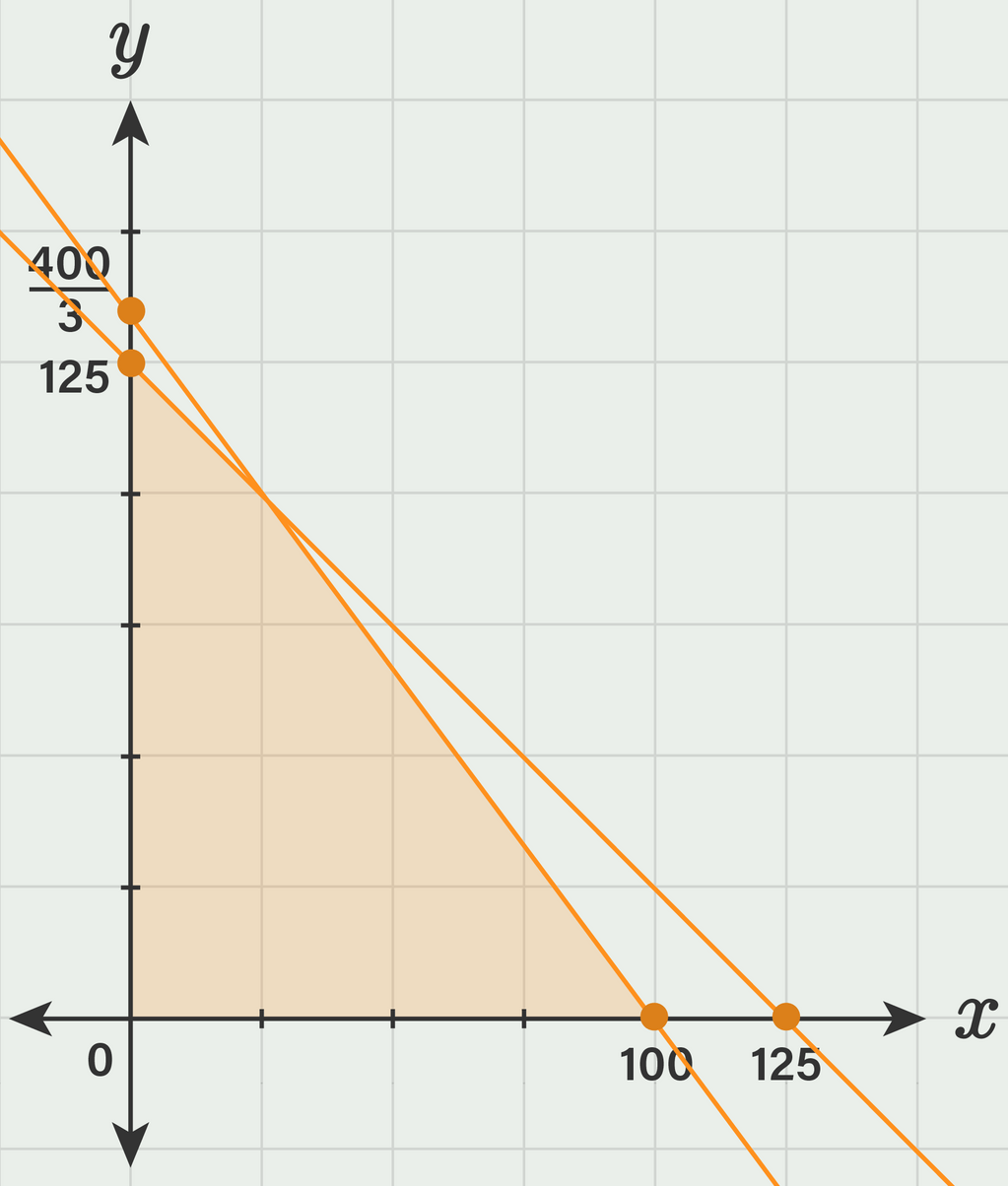
Seorang pengusaha perumahan mempunyai lahan tanah seluas 10.000 m 2 yang akan dibangun rumah tipe I dan tipe II. Rumah tipe I memerlukan tanah seluas 100 m 2 dan rumah tipe II memerlukan tanah seluas 75 m 2 . Jumlah rumah yang dibangun paling banyak 125 unit. Rumah tipe I dijual dengan harga Rp250.000.000,00 per unit dan rumah tipe II dijual dengan harga Rp200.000.000,00 per unit. Penghasilan maksimum yang dapat diperoleh pengusaha tersebut adalah...

Seorang pengusaha perumahan mempunyai lahan tanah seluas 10.000 m² yang akan dibangun rumah tipe I dan tipe II. Rumah tipe I memerlukan tanah seluas 100 m² dan rumah tipe II memerlukan tanah seluas 75 m². Jumlah rumah yang dibangun paling banyak 125 unit. Rumah tipe I dijual dengan harga Rp250.000.000,00 per unit dan rumah tipe II dijual dengan harga Rp200.000.000,00 per unit. Penghasilan maksimum yang dapat diperoleh pengusaha tersebut adalah...

Rp25.000.000.000,00
Rp26.250.000.000,00
Rp26.600.000.000,00
Rp26.670.000.000,00
Rp31.250.000.000,00

S. Nur

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang benar adalah B.

Pembahasan

Misalkan: Banyak rumah tipe I = x Banyak rumah tipe II= y Permasalahan pada soal dapat ditulis seperti berikut. Tanah seluas 10.000 m 2 akan dibangun rumah tipe I dan tipe II. Rumah tipe I memerlukan tanah seluas 100 m 2 dan rumah tipe II memerlukan tanah seluas 75 m 2 . Jumlah rumah yang dibangun paling banyak 125 unit Jumlah rumah, nilainya selalu positif Fungsi penghasilan maksimum: Sketsa grafik dari titik koordinat yang telah didapatkan. Titik potong kedua garis dicari dengan metode substitusi - eliminasi: Sehingga, titik koordinat titik potongnya adalah (25,100). Substitusikan 3titik koordinat daerah arsir ke . f ( x , y ) = 250.000.000 x + 200.000.000 y f ( 0 , 125 ) = 0 + 200.000.000 ( 125 ) = 25.000.000.000 f ( 100 , 0 ) = 250.000.000 ( 100 ) + 0 = 25.000.000.000 f ( 25 , 100 ) = 250.000.000 ( 25 ) + 200.000.000 ( 100 ) = 26.250.000.000 Dengan demikian, penghasilan maksimum yang didapatkan adalah Rp26.250.000.000 Oleh karena itu, jawaban yang benar adalah B.

Misalkan:

Banyak rumah tipe I = x

Banyak rumah tipe II = y

Permasalahan pada soal dapat ditulis seperti berikut.

Tanah seluas 10.000 m² akan dibangun rumah tipe I dan tipe II. Rumah tipe I memerlukan tanah seluas 100 m² dan rumah tipe II memerlukan tanah seluas 75 m².

100 x plus 75 y less or equal than 10.000 left right double arrow 4 x plus 3 y less or equal than 400 space x equals 0 rightwards arrow y equals 400 over 3 space left parenthesis 0 comma 400 over 3 right parenthesis y equals 0 rightwards arrow x equals 100 space left parenthesis 100 comma 0 right parenthesis

Jumlah rumah yang dibangun paling banyak 125 unit

x plus y less or equal than 125 x equals 0 rightwards arrow y equals 125 space left parenthesis 0 comma 125 right parenthesis y equals 0 rightwards arrow x equals 125 space left parenthesis 125 comma 0 right parenthesis

Jumlah rumah, nilainya selalu positif

open table attributes columnalign right end attributes row cell x greater or equal than 0 end cell row cell y greater or equal than 0 end cell end table close curly brackets space left parenthesis 0 comma 0 right parenthesis

Fungsi penghasilan maksimum:

f left parenthesis x comma y right parenthesis equals 250.000.000 x plus 200.000.000 y

Sketsa grafik dari titik koordinat yang telah didapatkan.

Titik potong kedua garis dicari dengan metode substitusi - eliminasi:

Sehingga, titik koordinat titik potongnya adalah (25,100).

Substitusikan 3 titik koordinat daerah arsir ke f left parenthesis x right parenthesis .

$f (x, y) = 250.000.000 x + 200.000.000 y f (0, 125) = 0 + 200.000.000 (125) = 25.000.000.000 f (100, 0) = 250.000.000 (100) + 0 = 25.000.000.000 f (25, 100) = 250.000.000 (25) + 200.000.000 (100) = 26.250.000.000$

Dengan demikian, penghasilan maksimum yang didapatkan adalah Rp26.250.000.000

Oleh karena itu, jawaban yang benar adalah B.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

390

4.5 (16 rating)

Florensia Elsaday

Pembahasan lengkap banget Ini yang aku cari! Bantu banget Mudah dimengerti Makasih ❤️

Zulvia Dini

Pembahasan tidak menjawab soal

Pertanyaan serupa

Suatu perusahaan transportasi harus mendistribusikan 1.200 paket (yang besarnya sama) melalui dua truk pengangkut. Truk 1 memuat 200 paket untuk setiap pengangkutan dan truk 2 memuat 80 paket untuk se...

4.5

Jawaban terverifikasi

Seorang pemilik toko sandal memiliki modal Rp4.000.000,00. Ia membeli setiap pasang sandal A Rp10.000,00 dan sandal B Rp8.000,00. Setiap pasang sandal A dan sandal B masing-masing memberi keuntungan R...

4.3

Jawaban terverifikasi

Misalkan kebutuhan air minum setiap minggu seseorang akan protein, karbohidrat, dan lemak masing-masing 8 unit, 12 unit, dan 9 unit. makanan jenis A per kg mengandung 2 unit protein, 6 unit karbihidra...

3.6

Jawaban terverifikasi

Pedagang tahu tempe keliling, belanja tahu yang harga belinya Rp500 dijual dengan harga Rp600 per buah. Sedangkan tempe yang harga belinya Rp750 dijual dengan harga Rp1.000. Apabila pedagang tersebut ...

1.0

Jawaban terverifikasi

Pensil merek A yang harga belinya Rp20.000,00 per kotak dijual dengan laba Rp4.000,00 per kotak, sedangkan pensil merek B yang harga belinya Rp10.000,00 per kotak dijual dengan laba Rp3.000,00 per kot...

4.7

Jawaban terverifikasi