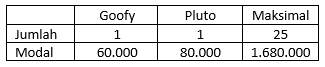
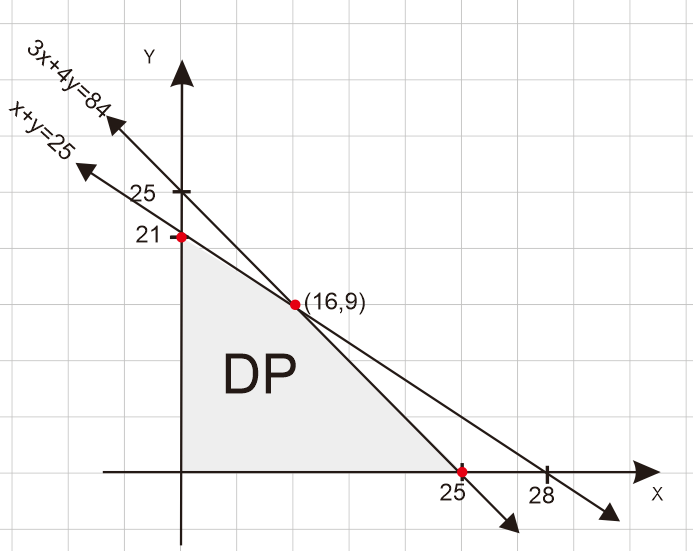
Seorang pengusaha mainan anak membeli beberapa boneka Goofy dan Pluto, tidak lebih darl 25 buah. Harga sebuah boneka Goofy Rp. 60.000,00 dan sebuah boneka Pluto Rp. 80.000,00. Modal yang dimiliki Rp. 1.680.000,00. Jika laba penjualan satu buah boneka Goofy Rp. 20.000,00 dan 1 buah boneka Pluto Rp. 25.000,00, maka laba maksimumnya adalah ...

Pembahasan

Menentukan sistem pertidaksamaan linearnyayaitu: Misalkan: x : Banyak Boneka Goofy y : Banyak Boneka Pluto Dengan menggunakan tabel maka kita dapat membuat model matematikanya Karena soal di atas merupakan banyak benda maka: Untuk fungsi objektif, laba penjualan satu buah boneka Goofy Rp. 20.000,00 dan 1 buah boneka Pluto Rp. 25.000,00 Menentukan titik potong garis dengan sumbu x dan sumbu y Untuk Titik potong terhadap sumbu x maka x + y x + ( 0 ) x ​ = = = ​ 25 25 25 ( 25 , 0 ) ​ Titik potong terhadap sumbu y maka x + y ( 0 ) + y y ​ = = = ​ 25 25 25 ( 0 , 25 ) ​ Untuk Titik potong terhadapsumbu x maka 3 x + 4 y 3 x + 0 x ​ = = = ​ 84 84 28 ( 28 , 0 ) ​ Titik potong terhadap sumbu y maka 3 x + 4 y 0 + 4 y y ​ = = = ​ 84 84 21 ( 0 , 21 ) ​ Selanjutnya, gambarkan daerah himpunan penyelesaiannya . Ingat : 0makaberlaku end text a x plus b y greater or equal than c space rightwards double arrow space text daerahpenyelesaiandikanangaris end text a x plus b y less or equal than c space rightwards double arrow space text daerahpenyelesaiandikirigaris end text" data-mathml="«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mtext»Jika§#160;a§#62;0§#160;maka§#160;berlaku§#160;«/mtext»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi»a«/mi»«mi»x«/mi»«mo»+«/mo»«mi»b«/mi»«mi»y«/mi»«mo»§#8805;«/mo»«mi»c«/mi»«mo»§#160;«/mo»«mo»§#8658;«/mo»«mo»§#160;«/mo»«mtext»daerah§#160;penyelesaian§#160;di§#160;kanan§#160;garis«/mtext»«mspace linebreak=¨newline¨/»«mspace linebreak=¨newline¨/»«mi»a«/mi»«mi»x«/mi»«mo»+«/mo»«mi»b«/mi»«mi»y«/mi»«mo»§#8804;«/mo»«mi»c«/mi»«mo»§#160;«/mo»«mo»§#8658;«/mo»«mo»§#160;«/mo»«mtext»daerah§#160;penyelesaian§#160;di§#160;kiri§#160;garis«/mtext»«/math»" role="math" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAVYAAABcCAYAAAA1Q51RAAAACXBIWXMAAA7EAAAOxAGVKw4bAAAABGJhU0UAAAAva/WvxwAADSZJREFUeNrtmwFkVt0fx6/HvCaPkcnMZCRJksjMJIlkkszIzCQzkiRJJHm98nqZV5JX4pUkmZEkySuSJHmN1yTJxCRJEskkM+P+f7/6Pv6n27n3nnOfc5+nte+Hr+259+yc3/mdc373d859FkWEEEIIIYQQQgghhBBCCCGEEEIIWR7EKb/bPjeCh6KtHuW17LRoQfREtK3JPvwR66un7phLhJCwC60Zi6pPdN8xwK4RzYi24LP+fIHrDKwMrIQwsGYE2L6UMhdEY4lro7jOwMrASsgPfxSwW3RH1GJc2yuawjb8tWgkpy3f8maAfWAJsLOiVYlr7aJXOf1dj/o+i56JDosOiJ6K5mHboIfdof2k9e1C/z6KhlPKDaM+PQrptNRROyZZzBjjevsWMxgTUiyw6gJ+JKom7k+INuD3bQgCWfiWNzlusW8xpexCTn+viHrxuQfXbuFaBUcK7z3sDu0nrW9StBr2nLcciwzgut4/hD4l67iLh0hW0Ku3bwyshBQIrEdEz5EJNmOb2Yfs0paxpgXWec82fYND2X5K3m9D1m7yFIE3QnC1BcT2AG3n9Y2BlZACgfW06LElU1G6RVdFcwhyeQvKp3wtoD6K0s9YX1iOAlZhCx0ysObZHdpPscPDYh7lalp0DG6xp215fWNgJaTgUcDB6OtLpNbEfT2fPCFa4bigXMqbATXvq1P6kmo0cU0/XwwcWPPsDu2n5P2u6OtZqck9UUeBrDj2tC2vb8ny6xlYCXF/eTUUfT2zMxfWJ9EmbEX3oHzWYncp7xJQa9S+brUZn3uRra4JHFjz7A7tJ70/LlqJevQcdGeizHbRDUvG7htY6+3bWzwM9e/3IVAzsJJlTQULyyWwKv2im9H/3wrrG+QPkG4Xz4neZbTnW94FDcL6jwELyOrygnKRwJpnd2g/zSFI6bmmfsNhR0q5ASOQuf5zR+w5Jnl92wMbFxB01zKwkuXOKLIhQgghdaIZkX6H807GVpIQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBClhWxY7lB0USA9vpFf4ralpn/losdS7lf8Q/Sx3iZjvVPNf9dDfpNdDJQm4dFM/jZLA4ysHLBLNE+MrAGokN0WzQveifqa8KgXhcNBGy3DZnrU9GOJvj0rGhS9AsDKwMrA+vyY4XouWgIn0+J9ifK3EoE25Wie6LOgIP0QrRX9J9oQXQicf8V2k3yr2hDRr1r8dC4I1qXY0OX6KJoTvSHxyTM0qMUu9MYE82Knon2WfynPpqCj16LRix1DOPetGWMtL6tuLfoUW8M/+m4fxa9FO128M0u9OeN6GhKuTx709qtou5K4m9aMF/aHOv3sWcQ9xYLjE2R8r4+d5lDPkcBu7F2WgLbXVbfR9F3TRCPFPS5bX3EHvPgC8eRXdW4ZMkcuxDwKsjAbiBgFQk0NiMqMPCyaDU+a4DbbJS5hs4kJ9BZx4D1KyZIGjvRRhcW7KVAD67JnHZNdCLoOXMrgvG4xV8TxoNkm+hj4r6O3Xn48JDoimV87orWe9YbY6EOoO5eBMu8BTppjOl5LHRfe7PavWBJBEYxf1zr97FHH7rdKf118WHZPneZQ66BdRiJQbUEu8vq+z94oGrCeKagz23rI/aYB194gAZqaKU9lnInoSuJgBciY+3FAJrsSWSNQ8ZiUdrh+GpO3bWM9XbGw2Al6motuM3K0kOPjHUGQahodhHh6GO18cCyTZz2AuMWW/zna1sb/OFrb1a767FrMZk2FoZL/T72zGAdtBb0Ydk+d5lDLnYcwU62WXOlSB0vHAKiS7vtDuVy58FHYytVQdpdsZRbg6xyewnnNfpkvGq59rfxuROT3sysRwKdsQ5Z2g9xxnrd84x1wcF/3bB1LmUbMp8I7IuO45FXb1xgbG33PwSwN3lNt4tb8HsfkoWi9eeV14X7WPQ2+voNlHp8WIbPFxyDR964nUY/qyXNlWb1vUi7tutZ8+ALT4yo22uZ+MoqVDKE9Dp0YP0L2y6T29H3L9Fmkf31WDJck8N42h5xtHG/ZctXL2MF/mY6+vZrYqst/nuG8+cVGUGmo8B45NUbIrB24binXnuT13Yb9U7gHK1o/XnlzTbf1unDMnzuModcx+0gdhitJdhdRt+nEg+CSqB2s67b5sEXzuD8sYIA9y5xv4rJttHIFHsCB9abovvGWdzRyP7y6ArOWaej9BdWte+x+rww6oTDN6H94SjsNyNcOYAxqKB/0xb/fTLs3IP7ZiDQHcUNPAx9xiOv3qKBdRxjoYvzmmXcithru/YcR1SzddafV77GRsuC8vVhGT53mUM+D8QhHA+2Bra7rL7Xzse7sWMM0W7W9Y1pgVXf9p3CYGzAedUw7uk2Vl+8bE2cbU4VPI9MQ4P5LmTPrzK2+DrI7yP3F1Y+dCDAq5OORc1jBD6YxUMittz/AOl27ZzlYTiAB0Xssajy6i0aWMfQHz2S2ZlSztde27VjaOdkgPrzysdoq79OH5bhc5c55LvT6MfaaAlod1l9192qvq1/Cbs/B2g38pwHUVqgrUQ/Jhr430TZL6z6cU5m062INJJGfh+yijO2NrqdGMzQBflcNbJpwsBqYn7FiixP9L2MeUyp705+p1uy0Uz0Pt2wpJhvYFvPoux/FCE/P/od6aeYd3ocMB59+48NhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCGEEEIIIYQQQgghhBBCCCFOxI7lBkUTJdqxQ/TnT+y/5WLHUu5X/IP0Ma7TzngJzJmfdb56d/A30ckS2l8rug2ta2C/DzKwMrAu0T4uB580hA4EnnnRO1FfEwb1umggYLttyFCfinY2wadnRZOiXxhYGVgZWJcfK0TPRUP4fEq0P1HmViLYrhTdE3UGHKQXor2i/0QLohOJ+6/QbpJ/RRsS1w6jT0dEFQ9fdIkuiuZEf3hMwiw9SrE7jTHRrOiZaJ/Ff+qjKfjotWjEUscw7k1bxkjr24p7ix71xsj4ddw/i16Kdjv4Zhf680Z0NKVcnr1p7VZRd3KMWzBf2hzr97FnEPcWC4xNkfK+PneZQz5bfW3vDnyadbRgm1Mua38Utr7Dei3iI5e2s8atFI4ju6pxyZI5diHgVZCB3cAWu0igsXWqgg5fFq3GZw1wm40y1+Cc5AQ6m7i2G4uq29MPO9FGFxbspUD+ncTEdEEnlp4ztyIYj1v8NWE8SLaJPibu69idhw8Pia5YxueuaL1nvTEW6gDq7kWwzFugk8aYnsdC97U3q90LlkRgFPPHtX4fe+Yy5paLD8v2ucsccg2sw0gMqjl/nzanYgdb/8EDUBO8MwV95NL2XIGYUBcPYHANNbLHUu4kdCUR8EJkrL0YQJM9iaxxyFgsSjsmXdVSn2asM/jpwkrU1Vpwm5Wlhx4Z6wyCUNHsIsLRx2rjgWWbiO0Fxi22PEx9bWuDP3ztzWp3PXYtJtPGQnOp38eeGayD1oI+LNvnLnPIxY4j2PW1O9rZXmDtvygQjIu27TNuQfhobKUq2HLYts9rkFVuL+G8Rp+MVy3X/jY+d2LSm5n1SEad5hnrjpz2hyzt14tm0tcjvzPWBQf/dcPWuZRtzXwisC86jkdevXGBsbXd/xDA3uQ13Spvwe99SBaK1p9XXgPBY9FbUX+dPizD5wuOwShv3E6jn9U66osbMN9d284at1J4YkTxXsvEV1bBqCGk66ED61/Ydpncjr5/iTaL7K/HkuGmsQ513cLDwcZ+y5avXsYK/M20cS4YIfNI+k8z6xPYOqUFmY4C45FXb4jA2oXjnnrtjS3HP5eNrePeOurPK2+2+bZOH5bhc5c55DpuB7HDaC0psE4lAnclkI+yrtvGrRQ0UP6KTmmAe5e4X8Vk22hkij2BA+tN0X3jLO5oZH95pMFvEJNng2c/d0bpL6Q6MYCb0P5wFPabEa4cwBhU0L9pi/8+GXbuwX0zEOiO4gYehj7jkVdv0cA6joehLs5rlnErYq/t2nMcUc3WWX9e+RobLQvU14dl+NxlDvk8EIdwPNhaQmBVW2vn2d3Y4YXwUdb1jY0KrPq27xQGYwPOq4ZxT7ex+uJla+JscyrwWYUG813Inl9lbPF1kN9H37+wCkEHArw6/VjUPEbgg1lsWWLL/Q+QbtfOWR6GA3hQxB6LIK/eooF1DP3J+tqbr722a8fQzskA9eeVj9FWf50+LMPnLnPId6fRj7XREjiwKvoeRN/Wv0Q7nwP4KPIct4bQEvl9RamRaOB/k3LuY06C+RTdikgjaeT3Ias4s2uj25c0M3RB47lqZNOEgdXE/IoVWRrouw/zWFHfdfxOtzQWzUTv0w1LivkGtvUs8j93J81Fv9P8FPNEjwPGo2//EWHJ8T84zeMtzCk2KgAAAnB0RVh0TWF0aE1MADxtYXRoIHhtbG5zPSJodHRwOi8vd3d3LnczLm9yZy8xOTk4L01hdGgvTWF0aE1MIj48bXRleHQ+SmlrYSYjeEEwO2EmZ3Q7MCYjeEEwO21ha2EmI3hBMDtiZXJsYWt1JiN4QTA7PC9tdGV4dD48bXNwYWNlIGxpbmVicmVhaz0ibmV3bGluZSIvPjxtc3BhY2UgbGluZWJyZWFrPSJuZXdsaW5lIi8+PG1pPmE8L21pPjxtaT54PC9taT48bW8+KzwvbW8+PG1pPmI8L21pPjxtaT55PC9taT48bW8+JiN4MjI2NTs8L21vPjxtaT5jPC9taT48bW8+JiN4QTA7PC9tbz48bW8+JiN4MjFEMjs8L21vPjxtbz4mI3hBMDs8L21vPjxtdGV4dD5kYWVyYWgmI3hBMDtwZW55ZWxlc2FpYW4mI3hBMDtkaSYjeEEwO2thbmFuJiN4QTA7Z2FyaXM8L210ZXh0Pjxtc3BhY2UgbGluZWJyZWFrPSJuZXdsaW5lIi8+PG1zcGFjZSBsaW5lYnJlYWs9Im5ld2xpbmUiLz48bWk+YTwvbWk+PG1pPng8L21pPjxtbz4rPC9tbz48bWk+YjwvbWk+PG1pPnk8L21pPjxtbz4mI3gyMjY0OzwvbW8+PG1pPmM8L21pPjxtbz4mI3hBMDs8L21vPjxtbz4mI3gyMUQyOzwvbW8+PG1vPiYjeEEwOzwvbW8+PG10ZXh0PmRhZXJhaCYjeEEwO3BlbnllbGVzYWlhbiYjeEEwO2RpJiN4QTA7a2lyaSYjeEEwO2dhcmlzPC9tdGV4dD48L21hdGg+2YR5JwAAAABJRU5ErkJggg=="> Daerah himpunan penyelesaian atau arsirannya ke kanandari sumbu . Daerah himpunan penyelesaian atau arsirannya ke atasdari sumbu . Terlebih dahulu gambar sistem pertidaksamaan tersebut diperoleh sebagai berikut: titik potong antara dua garis didapat dengan : Eliminasi persamaan pertama dan kedua: Subtitusi nilai x ke persamaan 1 Maka titiknya Kita uji nilai dari titik-titik sudut dari daerah penyelesaian tersebut dengan fungsi objektif: Untuk titik ( 0 , 0 ) z ​ = = = ​ 20.000 x + 25.000 y 20.000 ( 0 ) + 25.000 ( 0 ) 0 ​ Untuk titik z ​ = = = ​ 20.000 x + 25.000 y 20.000 ( 25 ) + 0 Rp 500.000 ​ Untuk titik z ​ = = = ​ 20.000 x + 25.000 y 0 + 25.000 ( 21 ) Rp 525.000 ​ Untuk titik Dengan demikian, laba maksimum adalah Rp 545.000,00. Jadi, jawaban yang tepat adalah A