Pertanyaan

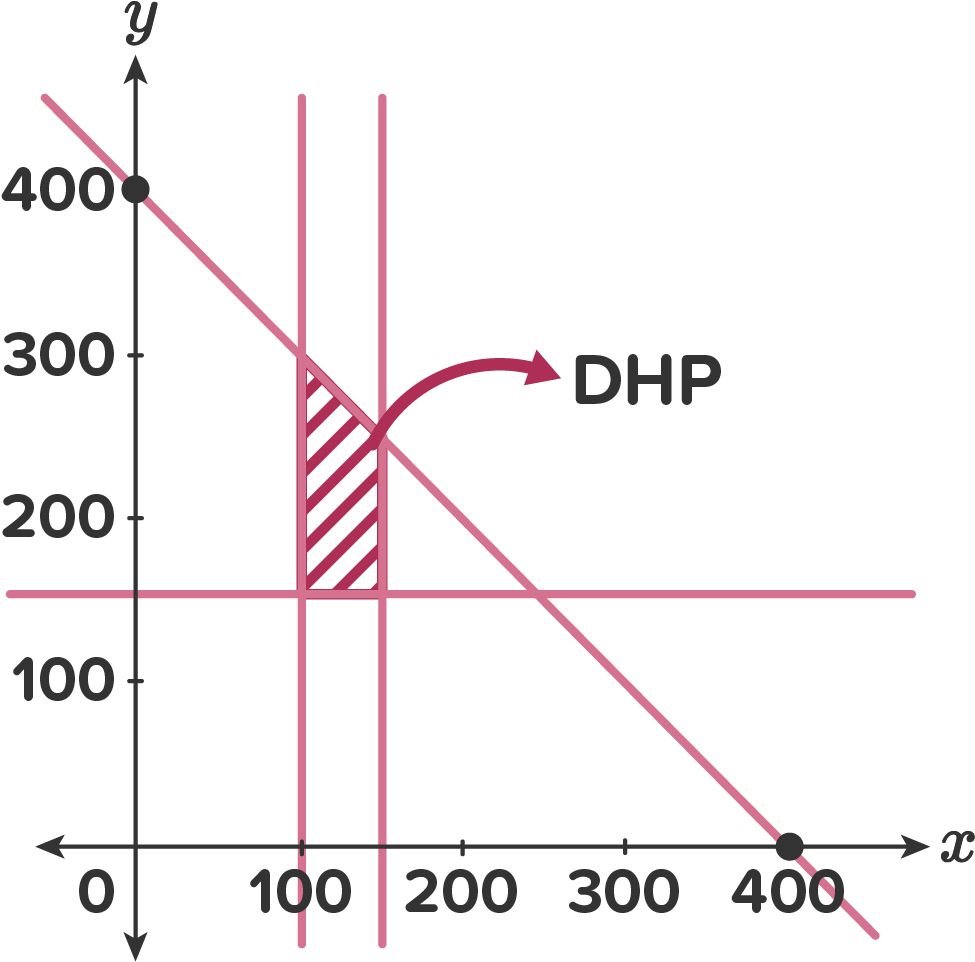
Seorang pemilik kios bunga ingin mengisi kiosnya dengan bibit bunga mawar paling sedikit 100 pohon tetapi tidak lebih dari 150 pohon. Bibit bunga melati paling sedikit 150 pohon. Kios tersebut hanya memuat 400 bibit pohon. Keuntungan satu bibit bunga mawar Rp 2.000,00 dan satu bunga melati Rp 1.000,00. Jika banyak bibit bunga mawar tidak boleh lebih dari 150, kuntungan maksimum yang didapat adalah …

Seorang pemilik kios bunga ingin mengisi kiosnya dengan bibit bunga mawar paling sedikit 100 pohon tetapi tidak lebih dari 150 pohon. Bibit bunga melati paling sedikit 150 pohon. Kios tersebut hanya memuat 400 bibit pohon. Keuntungan satu bibit bunga mawar Rp 2.000,00 dan satu bunga melati Rp 1.000,00. Jika banyak bibit bunga mawar tidak boleh lebih dari 150, kuntungan maksimum yang didapat adalah $\dots$

Rp 350.000,00
Rp 400.000,00
Rp 450.000,00
Rp 550.000,00
Rp 650.000,00

R. Septa

Master Teacher

Mahasiswa/Alumni Universitas Negeri Malang

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah D.

Pembahasan

Misalkan banyak bibit bunga mawar adalah x , dan banyak bibit bunga melati adalah y , maka sistem pertidaksamaan yang memenuhi adalah sebagai berikut: Fungsi objektifnya adalah . Jika digambarkan, daerah penyelesaian untuk sistem pertidaksamaan linear di atas adalah sebagai berikut: Daerah himpunan penyelesaian tersebut mempunyai 4 titik ujung yaitu titik (100,150), (100,300), (150,150), dan (150,250). Substitusi titik-titik tersebut ke fungsi objektif. Sehingga didapat keuntungan maksimumnya sebesar Rp 550.000,00. Jadi, jawaban yang tepat adalah D.

Misalkan banyak bibit bunga mawar adalah x, dan banyak bibit bunga melati adalah y, maka sistem pertidaksamaan yang memenuhi adalah sebagai berikut:

Fungsi objektifnya adalah .

Jika digambarkan, daerah penyelesaian untuk sistem pertidaksamaan linear di atas adalah sebagai berikut:

Daerah himpunan penyelesaian tersebut mempunyai 4 titik ujung yaitu titik (100,150), (100,300), (150,150), dan (150,250).

Substitusi titik-titik tersebut ke fungsi objektif.

Sehingga didapat keuntungan maksimumnya sebesar Rp 550.000,00.

Jadi, jawaban yang tepat adalah D.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

452

5.0 (1 rating)

Pertanyaan serupa

Seorang pemilik toko sandal memiliki modal Rp4.000.000,00. Ia membeli setiap pasang sandal A Rp10.000,00 dan sandal B Rp8.000,00. Setiap pasang sandal A dan sandal B masing-masing memberi keuntungan R...

4.3

Jawaban terverifikasi

Sebuah pesawat terbang dapat menampung 300 penumpang. Penumpang kelas eksekutif dapat membawa 50 kg bagasi dan penumpang kelas ekonomi dapat membawa 30 kg bagasi. Pesawat tersebut hanya dapat membawa ...

0.0

Jawaban terverifikasi

Sebuah pabrik memproduksi biskuit yang dikemas dalam bentuk kaleng kemasan 1kg dan 2kg . Kapasitas produk setiap harinya tidak lebih dari 120 kaleng. Setiap hari, biskuit dengan kemasan diproduksi tid...

5.0

Jawaban terverifikasi

Seorang penjual buah menginginkan dalam sehari dapat menjual minimal 300 buah. Buah yang dijualnya adalah pepaya dan semangka. Keuntungan dari satu buah pepaya adalah Rp5.000 dan dari satu buah semang...

0.0

Jawaban terverifikasi

Suatu pengembang perumahan mempunyai tanah seluas 10.000m 2 yang akan dibangun tidak lebih dari 125 unit untuk rumah tipe 36 dan tipe 45 . Rumah tipe dan tipe memerlukan luas tanah berturut-turut 75m ...

3.0

Jawaban terverifikasi