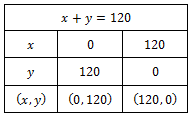Iklan
Pertanyaan
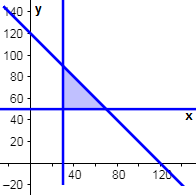
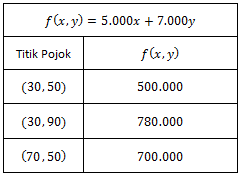
Sebuah pabrik memproduksi biskuit yang dikemas dalam bentuk kaleng kemasan 1kg dan 2kg . Kapasitas produk setiap harinya tidak lebih dari 120 kaleng. Setiap hari, biskuit dengan kemasan diproduksi tidak kurang dari 30 kaleng dan kemasan tidak kurang dari 50 kaleng. Keuntungan dari penjualan biskuit kemasan sebesar Rp5.000,00 per kaleng dan untuk kemasan sebesar Rp7.000,00 . Misalkan, banyak produksi setiap kemasan berturut-turut adalah x dan y . Tentukan: b. banyak produksi setiap jenis agar diperoleh keuntungan maksimum dan tentukan besar keuntungan maksimumnya.
Sebuah pabrik memproduksi biskuit yang dikemas dalam bentuk kaleng kemasan dan . Kapasitas produk setiap harinya tidak lebih dari kaleng. Setiap hari, biskuit dengan kemasan diproduksi tidak kurang dari kaleng dan kemasan
tidak kurang dari kaleng. Keuntungan dari penjualan biskuit kemasan
sebesar per kaleng dan untuk kemasan
sebesar . Misalkan, banyak produksi setiap kemasan berturut-turut adalah dan . Tentukan:
b. banyak produksi setiap jenis agar diperoleh keuntungan maksimum dan tentukan besar keuntungan maksimumnya.
Iklan
S. Nur
Master Teacher
10
5.0 (1 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia