Pertanyaan

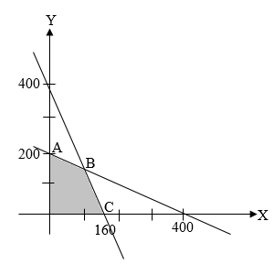
Seorang pembuat kue mempunyai 8.000 gr tepung dan 2.000 gr gula pasir. Ia ingin membuat dua macam kue yaitu kue dadar dan kue apem. Untuk membuat kue dadar dibutuhkan 5 gram gula pasir dan 50 gram tepung sedangkan untuk membuat kue apem dibutuhkan 10 gram gula pasir dan 20 gram tepung. Jika kue dadar dijual dengan harga Rp1.000,00/buah dan kue apem dijual dengan harga Rp1.500,00/buah. Pendapatan maksimum yang dapat diperoleh pembuat kue tersebut adalah....

Rp160.000,00
Rp200.000,00
Rp300.000,00
Rp325.000,00
Rp350.000,00

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

S. Intan

Master Teacher

Mahasiswa/Alumni Institut Pertanian Bogor

Jawaban terverifikasi

Jawaban

keuntungan maksimum yang diperoleh oleh pembuat kue adalah Rp325.000,00.

Pembahasan

Jumlah kue dadar = Jumlah kue apem = Dari tabel di atas dapat disusun sistem pertidaksamaan linear sebagai berikut: Dengan fungsi objektif Kemudian gambarkan sistem pertidaksamaan yang sudah disusun dalam grafik. Untuk garis Untuk garis Titik A (0, 200) Titik C (160, 0) Titik B merupakan titik potong garis dan Substitusi nilai x ke persamaan Jadi, titik B (100, 150) Selanjutkan substitusikan titik A, B, dan C ke fungsi objektif : Jadi, keuntungan maksimum yang diperoleh oleh pembuat kue adalah Rp325.000,00.

Jumlah kue dadar =

Jumlah kue apem =

Dari tabel di atas dapat disusun sistem pertidaksamaan linear sebagai berikut:

50 x plus 20 y equals 8000 rightwards arrow 5 x plus 2 y less or equal than 800 5 x plus 10 y equals 2000 rightwards arrow x plus 2 y less or equal than 400 x greater or equal than 0 semicolon space y greater or equal than 0

Dengan fungsi objektif

Kemudian gambarkan sistem pertidaksamaan yang sudah disusun dalam grafik.

Untuk garis

Titik A (0, 200)

Titik C (160, 0)

Titik B merupakan titik potong garis dan

$5 x plus 2 y equals 800 fraction numerator x plus 2 y equals 400 over denominator space space space space space space 4 x equals 400 end fraction space space space space space space space space space x equals 100$

Substitusi nilai x ke persamaan

100 plus 2 y equals 400 space space space space space space space space space space space 2 y equals 400 minus 100 space space space space space space space space space space space 2 y equals 300 space space space space space space space space space space space space space space y equals 150

Jadi, titik B (100, 150)

Selanjutkan substitusikan titik A, B, dan C ke fungsi objektif :

Jadi, keuntungan maksimum yang diperoleh oleh pembuat kue adalah Rp325.000,00.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.5 (11 rating)

Susana Abigail

Makasih ❤️

Maria

Pembahasan lengkap banget Mudah dimengerti

Rosiana Isnaini

Ini yang aku cari! Pembahasan lengkap banget Makasih ❤️

Kezia Agustina Lumbangaol

Pembahasan lengkap banget Mudah dimengerti Bantu banget Makasih ❤️

Muhamad Rafi

Jawaban tidak sesuai

Pertanyaan serupa

Tujuh puluh anggota PRAMUKA akan mengadakan kegiatan perkemahan dengan menggunakan dua buah jenis tenda. Tenda jenis I dapat menampung 7 orang, dan tenda jenis II dapat menampung 2 orang. Harga sewa u...

4.5

Jawaban terverifikasi

Seorang ibu memproduksi dua jenis keripik pisang, yaitu rasa coklat dan rasa keju. Setiap kilogram keripik rasa coklat membutuhkan modal Rp10.000,00 per kilogram, sedangkan keripik rasa keju membutuhk...

4.3

Jawaban terverifikasi

Untuk membuat satu bungkus roti A diperlukan 50 gram mentega dan 40 gram tepung, sedangkan untuk membuat satu roti B diperlukan 100 gram mentega dan 20 gram tepung. Jika tersedia 3,5 kg mentega dan 2,...

4.8

Jawaban terverifikasi

Seorang pedagang buah menjual dua jenis buah yaitu buah mangga dan buah lengkeng. Buah mangga ia beli dengan harga Rp12.000,00 per kilogram dan ia jual dengan harga Rp16.000,00 per kilogram. Sedangkan...

4.8

Jawaban terverifikasi

Seorang pedagang menjual minuman jenis A dengan harga Rp2.000,00 per botol dan minuman jenis B dengan harga Rp1.000,00 per botol. Dari minuman jenis A dan B yang dijualnya, Ia mendapatkan laba sebesar...

3.0

Jawaban terverifikasi