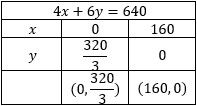
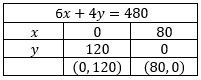
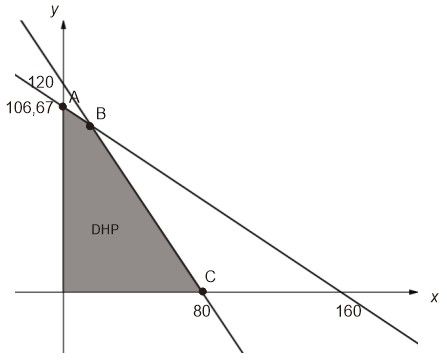
Seorang pemborong mendapat pesanan dua jenis bentuk pagar, yaitu jenis I seharga Rp 30.000 , 00/ m dan pagar jenis II seharga Rp 45.000 , 00/ m . Tiap m 2 pagar jenis I memerlukan 4 m besi pipa dan 6 m besi beton. Tiap pagar jenis II memerlukan 8 m besi pipa dan besi beton. Persediaan yang ada 640 m besi pipa dan 480 besi beton. Jika semua pesanan terpeuhi, maka hasil penjualan maksimum kedua jenis pagar adalah ...

Pembahasan

Langkah pertama, pertama kita misalkan pagar jenis I dan pagar jenis II. Diperoleh dua fungsi yang tak mungkin negatif, yaitu dan . Langkah kedua adalah membentuk sistem pertidaksamaan dari soal yang diketahui. Untuk memudahkan, kita buat dulu tabelnya. Diperoleh sistem pertidaksamaan: Langkah ketiga adalah menentukan fungsi tujuan yang dioptimumkan. Dari soal tersebut, ditanyakan hasil penjualan maksimum kedua jenis pagar tersebut, dan diketahui bahwa pagar jenis I mempunyai harga dan pagar jenis II mempunyai harga . Sehingga, diperoleh fungsi tujuan (dalam ribuan). Langkah keempat adalah menggambar daerah himpunan penyelesaian dengan uji titik pada sistem pertidaksamaan yang didapatkan. Setiap persamaan garis dapat digambar dengan mencari titik potong sumbu X dan sumbu Y. Berikut tabel titik potongnya. Grafik beserta daerah himpunan penyelesaiannya adalah: Titik B didapatkan dari titik potong antara kedua garis dan dapat dicari dengan substitusi dan eliminasi. Diperoleh titik . Langkah berikutnya adalah menghitung nilai dari fungsi tujuan dengan uji titik pojok. Berikut tabel uji titik pojoknya. Jadi, hasil penjualan maksimumnya adalah Rp4.800.000,00. Oleh karena itu, jawaban yang benar adalah D.