Pertanyaan

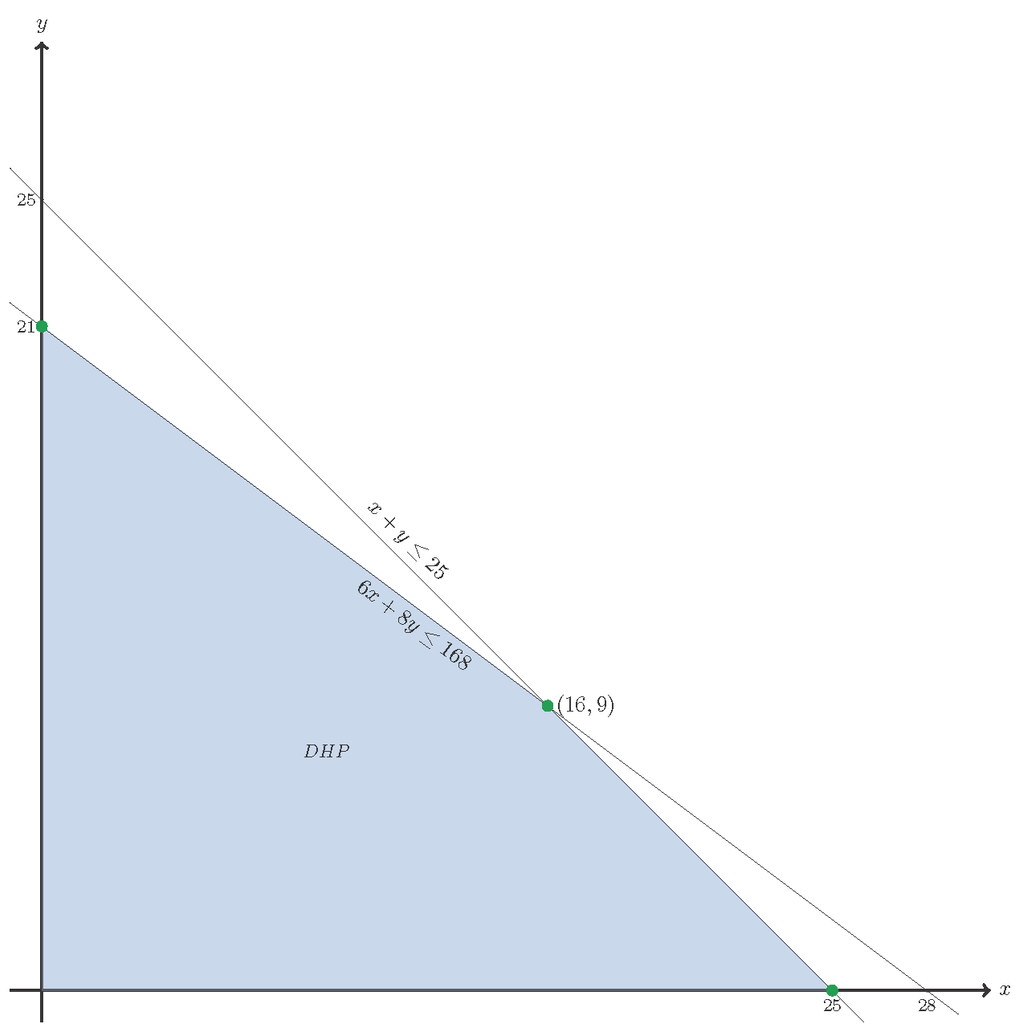
Seorang pedagang mainan akan membeli beberapa boneka dan mobil-mobilan tidak lebih dari 25 buah. Harga sebuah boneka Rp60.000,00 dan mobil-mobilan Rp80.000,00. Modal yang dimilikinya Rp1.680.000,00. Jika laba penjualan sebuah boneka Rp20.000,00 dan sebuah mobil-mobilan Rp25.000,00 maka keuntungan maksimum pedagang tersebut adalah ...

Rp545.000,00
Rp525.000,00
Rp500.000,00
Rp400.000,00
Rp350.000,00

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

W. Wati

Master Teacher

Jawaban terverifikasi

Jawaban

jawaban yang benar adalah A.

Pembahasan

Ingat materi program linear untuk menyelesaikan soal cerita seperti pada soal. Misalkan boneka sebagai dan mobil-mobilan sebagai . Maksimal banyak barang yang dibeli 25 buah: x + y ≤ 25 … ( 1 ) Modal yang dimiliki: 60.000 x + 80.000 y 6 x + 8 y ≤ ≤ 1.680.000 168 … ( 2 ) Fungsi objektif adalah keuntungan dari penjualan. Membuat sketsa grafik dari persamaan (1) dan (2) dengan mencari titik potong-titik potongnya dengan mengubah pertidaksamaan yang ada menjadi sebuah persamaan. Persamaan (1) titik potong sumbu , Didapat titik potong (25,0) titik potong sumbu , Didapat titik potong (0,25) Persmaaan (2) titik potong sumbu , Didapat titik potong (28,0) titik potong sumbu , Didapat titik potong (0,21) Persamaan (1) Substitusi (3) ke , didapat Substitusi (4) ke (3) Didapat titik potong (16,9) Berikut lukisan atau sketsa kedua garis dan titik potongnya beserta titik-titik kritisnya. Selanjutnya melakukan uji titik untuk mendapatkan fungsi objektif maksimum: Dari perhitungan di atas didapatkan bahwa fungsi objektif bernilai maksimum pada titik (16,9) dengan hasil 545.000. sehingga keuntungan maksimum pedagang adalah Rp545.000,00. Oleh karena itu, jawaban yang benar adalah A.

Ingat materi program linear untuk menyelesaikan soal cerita seperti pada soal. Misalkan boneka sebagai dan mobil-mobilan sebagai .

Maksimal banyak barang yang dibeli 25 buah:

$x + y \leq 25 \dots (1)$

Modal yang dimiliki:

$60.000 x + 80.000 y 6 x + 8 y \leq \leq 1.680.000 168 \dots (2)$

Fungsi objektif adalah keuntungan dari penjualan.

f open parentheses x comma y close parentheses equals 20.000 x plus 25.000 y

Membuat sketsa grafik dari persamaan (1) dan (2) dengan mencari titik potong-titik potongnya dengan mengubah pertidaksamaan yang ada menjadi sebuah persamaan.

Persamaan (1)

x plus y equals 25 titik potong sumbu , y equals 0

table attributes columnalign right center left columnspacing 0px end attributes row cell x plus y end cell equals 25 row cell x plus 0 end cell equals 25 row x equals 25 end table

Didapat titik potong (25,0)

x plus y equals 25 titik potong sumbu , x equals 0

table attributes columnalign right center left columnspacing 0px end attributes row cell x plus y end cell equals 25 row cell 0 plus y end cell equals 25 row y equals 25 end table

Didapat titik potong (0,25)

Persmaaan (2)

6 x plus 8 y equals 168 titik potong sumbu , y equals 0

table attributes columnalign right center left columnspacing 0px end attributes row cell 6 x plus 8 y end cell equals 168 row cell 6 x plus 8 left parenthesis 0 right parenthesis end cell equals 168 row cell 6 x end cell equals 168 row x equals cell 168 over 6 end cell row x equals 28 end table

Didapat titik potong (28,0)

6 x plus 8 y equals 168 titik potong sumbu , x equals 0

table attributes columnalign right center left columnspacing 0px end attributes row cell 6 x plus 8 y end cell equals 168 row cell 6 left parenthesis 0 right parenthesis plus 8 y end cell equals 168 row cell 8 y end cell equals 168 row y equals cell 168 over 8 end cell row y equals 21 end table

Didapat titik potong (0,21)

Persamaan (1)

table attributes columnalign right center left columnspacing 0px end attributes row cell x plus y end cell equals 25 row x equals cell 25 minus y horizontal ellipsis left parenthesis 3 right parenthesis end cell end table

Substitusi (3) ke 6 x plus 8 y equals 168 , didapat

Substitusi (4) ke (3)

table attributes columnalign right center left columnspacing 0px end attributes row x equals cell 25 minus y end cell row x equals cell 25 minus 9 end cell row x equals 16 end table

Didapat titik potong (16,9)

Berikut lukisan atau sketsa kedua garis dan titik potongnya beserta titik-titik kritisnya.

Selanjutnya melakukan uji titik untuk mendapatkan fungsi objektif maksimum:

Dari perhitungan di atas didapatkan bahwa fungsi objektif bernilai maksimum pada titik (16,9) dengan hasil 545.000. sehingga keuntungan maksimum pedagang adalah Rp545.000,00.

Oleh karena itu, jawaban yang benar adalah A.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

1.0 (1 rating)

Nain Nia

Jawaban tidak sesuai

Pertanyaan serupa

Pensil merek A yang harga belinya Rp20.000,00 per kotak dijual dengan laba Rp4.000,00 per kotak, sedangkan pensil merek B yang harga belinya Rp10.000,00 per kotak dijual dengan laba Rp3.000,00 per kot...

4.7

Jawaban terverifikasi

Setiap hari, seorang pembuat kue membuat dua jenis kue untuk dijual. Biaya pembuatan setiap kue jenis A adalah Rp 20.000 , 00 dan keuntungannya Rp 8.000 , 00 . Sementara itu, biaya pembuatan setiap ku...

5.0

Jawaban terverifikasi

Seorang pemilik toko sepatu ingin mengisi tokonya dengan sepatu laki-laki paling sedikit 100 pasang dan sepatu perempuan paling sedikit 150 pasang. Tokonya dapat diisi dengan paling banyak 400 pasang ...

3.6

Jawaban terverifikasi

0.0

Jawaban terverifikasi

Tempat parkir seluas 176 m 2 dapat menampung tidak lebih dari 20 kendaraan dari jenis sedan dan bus. Rata-rata luas lahan parkir untuk sebuah sedan adalah 4 m 2 dan untuk sebuah bus 20 m 2 .Biaya park...

2.0

Jawaban terverifikasi