Selesaikan: d. x2−5x+6(x−1)2≤0

Pertanyaan

Selesaikan:

d. $fraction numerator open parentheses x minus 1 close parentheses squared over denominator x squared minus 5 x plus 6 end fraction less or equal than 0$

N. Puspita

Master Teacher

Jawaban terverifikasi

Jawaban

himpunan penyelesaiannya adalah H p equals open curly brackets x vertical line 2 less than x less than 3 close curly brackets

Pembahasan

Pertidaksamaan tersebut merupakan pertidaksamaan rasional, syaratnya penyebut tidak boleh sama dengan nol.

$space space space fraction numerator open parentheses x minus 1 close parentheses squared over denominator x squared minus 5 x plus 6 end fraction less or equal than 0 fraction numerator open parentheses x minus 1 close parentheses squared over denominator open parentheses x minus 3 close parentheses open parentheses x minus 2 close parentheses end fraction less or equal than 0$

Pembuat nol pada pembilang: x equals 1

Pembuat nol pada penyebut: x equals 3 space atau space x equals 2

Kemudian kita buat garis bilangan, dan kita tentukan tanda disetiap daerahnya dengan cara kita uji titik. Misal kita ambil $x=5$ , kemudian kita susbstitusi

$table attributes columnalign right center left columnspacing 2px end attributes row cell fraction numerator open parentheses x minus 1 close parentheses squared over denominator open parentheses x minus 3 close parentheses open parentheses x minus 2 close parentheses end fraction end cell equals cell fraction numerator open parentheses 5 minus 1 close parentheses squared over denominator open parentheses 5 minus 3 close parentheses open parentheses 5 minus 2 close parentheses end fraction end cell row blank equals cell fraction numerator 16 over denominator open parentheses 2 close parentheses open parentheses 3 close parentheses end fraction end cell row blank equals cell 16 over 6 end cell end table$

maka kita peroleh nilai yang positif, sehingga tanda daerah disebelah kanan $x=3$ adalah positif. Begitu seterusnya, dan kita peroleh garis bilangan berikut ini.

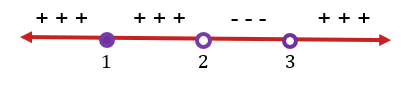
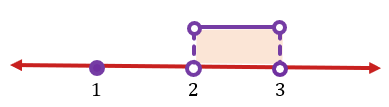
karena tanda pertidaksamaan kita adalah " less or equal than " , maka pada garis bilangan kita ambil daerah yang bernilai negatif. Dan karena penyebut tidak boleh sama dengan nol, maka penyelesaiannya adalah: