Pertanyaan

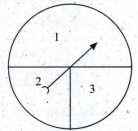
Sebuah papan lingkaran yang bisa diputar terhadap porosnya dibagi menjadi 3 daerah yang ukurannya tampak seperti pada gambar. Jika papan berotasi 5 kali, berapa probabilitas jarum menunjuk: c. ke daerah berangka 2 lebih dari 1 kali?

Sebuah papan lingkaran yang bisa diputar terhadap porosnya dibagi menjadi $3$ daerah yang ukurannya tampak seperti pada gambar. Jika papan berotasi $5$ kali, berapa probabilitas jarum menunjuk:

c. ke daerah berangka $2$ lebih dari $1$ kali?

8 dari 10 siswa nilainya naik

dengan paket belajar pilihan

Habis dalam

Klaim

D. Rajib

Master Teacher

Mahasiswa/Alumni Universitas Muhammadiyah Malang

Jawaban terverifikasi

Jawaban

probabilitas jarum menunjuk ke daerah berangka 2 lebih dari 1 kali adalah 0 , 367.

probabilitas jarum menunjuk ke daerah berangka

2

lebih dari

1

kali adalah

0, 367.

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah 0 , 367 . Ingat P ( X , n ) = C ( n , x ) ⋅ p x ⋅ q n − x Keterangan: P ( X , n ) = probabilitas kejadian X dalam n percobaan X = kejadian sukses C = kombinasi p = probabilitas sukses q = probabilitas gagal n = banyak percobaan x = banyak kejadian sukses Diketahui sebuah papan lingkaran yang bisa diputar terhadap porosnya dibagi menjadi 3 daerah yang ukurannya tampak seperti pada gambar. daerah berangka 1 memiliki luas 2 1 bagian maka peluangnya 2 1 daerah berangka 2 memiliki luas 4 1 bagianmaka peluangnya 4 1 daerah berangka 2 memiliki luas 4 1 bagianmaka peluangnya 4 1 Papan berotasi lima kali, artinya n = 5. Maka diperoleh probabilitas jarum menunjuk ke daerah berangka 2 lebih dari 1 kali sebagai berikut. misal kejadian sukses diasumsi sebagai "jarum menunjuk ke daerah berangka 2 " maka peluang sukses = p = 4 1 , berarti q = 1 − p = 4 3 P ( X > 1 ) = 1 − P ( X ≤ 1 ) = 1 − P ( X = 0 ) − P ( X = 1 ) ⇔ P ( X = 0 ) = P ( x = 0 , n = 5 ) = C ( 5 , 0 ) ⋅ ( 4 1 ) 0 ⋅ ( 4 3 ) 5 − 0 = 5 ! 0 ! 5 ! ⋅ ( 4 3 ) 5 = 1024 243 ⇔ P ( X = 1 ) = P ( x = 1 , n = 5 ) = C ( 5 , 1 ) ⋅ ( 4 1 ) 1 ⋅ ( 4 3 ) 5 − 1 = 4 ! 1 ! 5 ! ⋅ 4 5 81 = 1024 405 P ( X > 1 ) = 1 − P ( X = 0 ) − P ( X = 1 ) = 1 − 1024 243 − 1024 405 = 1024 376 = 0 , 367 Dengan demikian, probabilitas jarum menunjuk ke daerah berangka 2 lebih dari 1 kali adalah 0 , 367.

Jawaban yang benar untuk pertanyaan tersebut adalah $0, 367 .$

Ingat $P (X, n) = C (n, x) \cdot p^{x} \cdot q^{n - x}$

Keterangan:

$P (X, n) =$ probabilitas kejadian $X$ dalam $n$ percobaan

$X =$ kejadian sukses

$C =$ kombinasi

$p =$ probabilitas sukses

$q =$ probabilitas gagal

$n =$ banyak percobaan

$x =$ banyak kejadian sukses

Diketahui sebuah papan lingkaran yang bisa diputar terhadap porosnya dibagi menjadi $3$ daerah yang ukurannya tampak seperti pada gambar.

daerah berangka $1$ memiliki luas $\frac{1}{2}$ bagian maka peluangnya $\frac{1}{2}$
daerah berangka $2$ memiliki luas $\frac{1}{4}$ bagian maka peluangnya $\frac{1}{4}$
daerah berangka $2$ memiliki luas $\frac{1}{4}$ bagian maka peluangnya $\frac{1}{4}$

Papan berotasi lima kali, artinya $n = 5.$
Maka diperoleh probabilitas jarum menunjuk ke daerah berangka $2$ lebih dari $1$ kali sebagai berikut.
misal kejadian sukses diasumsi sebagai "jarum menunjuk ke daerah berangka $2$ " maka peluang sukses $= p = \frac{1}{4},$ berarti $q = 1 - p = \frac{3}{4}$

$P (X > 1) = 1 - P (X \leq 1) = 1 - P (X = 0) - P (X = 1)$
$\Leftrightarrow P (X = 0) = P (x = 0, n = 5) = C (5, 0) \cdot (\frac{1}{4})^{0} \cdot (\frac{3}{4})^{5 - 0} = \frac{5 !}{5 ! 0 !} \cdot (\frac{3}{4})^{5} = \frac{243}{1024}$
$\Leftrightarrow P (X = 1) = P (x = 1, n = 5) = C (5, 1) \cdot (\frac{1}{4})^{1} \cdot (\frac{3}{4})^{5 - 1} = \frac{5 !}{4 ! 1 !} \cdot \frac{81}{4 ^{5}} = \frac{405}{1024}$

$P (X > 1) = 1 - P (X = 0) - P (X = 1) = 1 - \frac{243}{1024} - \frac{405}{1024} = \frac{376}{1024} = 0, 367$

Dengan demikian, probabilitas jarum menunjuk ke daerah berangka $2$ lebih dari $1$ kali adalah $0, 367.$

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (7 rating)

Syifa Azzahra

Pembahasan lengkap banget

Naufal Aulia Pratama

Pembahasan terpotong

Pertanyaan serupa

Variabel acak x memiliki distribusi binomial B ( n , 0 , 8 ) dengan n menyatakan banyak percobaan ulang dan 0 , 8 adalah peluang sukses untuk x . Tentukan kumpulan nilai-nilai yang mungkin dari n sede...

5.0

Jawaban terverifikasi

Dalam suatu tes, peserta diminta mengerjakan 10 soal pilihan ganda dengan 4 opsi jawaban yaitu A, B, C, dan D. Tentukan peluang seorang peserta tes menjawab dengan benar: c. 8 soal

3.6

Jawaban terverifikasi

Menurut teori genetik, suatu jenis kelinci tertentu akan menghasilkan anak berbulu cokelat, hitam, dan putih dalam rasio 2 : 1 : 1 . Dari sekumpulan anak kelinci tersebut, dipilih 8 anak kelinci secar...

5.0

Jawaban terverifikasi

Pada mata pelajaran tertentu diketahui peluang seorang guru datang pada setiap pertemuannya sebesar 0 , 8 . Dari 20 kali tatap muka, tentukan peluang guru tersebut: a. paling banyak masuk 16 kali ...

4.9

Jawaban terverifikasi

Sepuluh persen produksi baut ternyata rusak. Baut-baut tersebut dijual dalam kotak. Setiap kotak berisi 25 buah. Tentukan peluang sebuah kotak akan berisi: 2. Tidak lebihdari dua baut rusak

5.0

Jawaban terverifikasi