Iklan
Pertanyaan
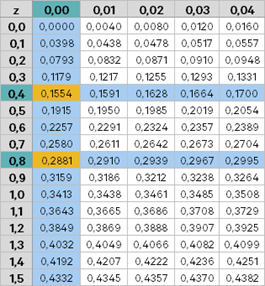
Sebuah mesin memproduksi paku yang panjang pakunya berdistribusi Normal dengan rata-rata 10 cm dengan standar deviasi 2,5 cm. Paku yang lulus uji untuk dijual adalah paku yang panjangnya antara 8 – 11 cm. Jika dipilih satu paku secara acak, maka probabilitas terpilih paku yang tidak lulus uji untuk dijual adalah ....
Sebuah mesin memproduksi paku yang panjang pakunya berdistribusi Normal dengan rata-rata 10 cm dengan standar deviasi 2,5 cm. Paku yang lulus uji untuk dijual adalah paku yang panjangnya antara 8 – 11 cm. Jika dipilih satu paku secara acak, maka probabilitas terpilih paku yang tidak lulus uji untuk dijual adalah ....
0,2881
0,3673
0,4435
0,5565
0,6327
Iklan
SI
S. Intan
Master Teacher
Mahasiswa/Alumni Institut Pertanian Bogor
Jawaban terverifikasi
1
1.0 (1 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia