Sebuah kubus ABCD.EFGH memiliki panjang rusuk 6 cm dengan P adalah titik pada HG sehingga HP = 2 1 ​ HG . Jarak antara titik A dan titik P adalah … cm .

Pembahasan

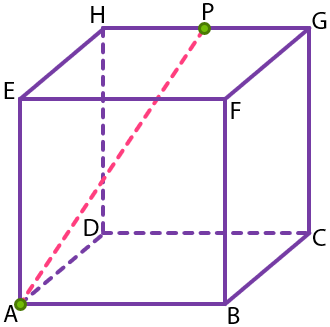
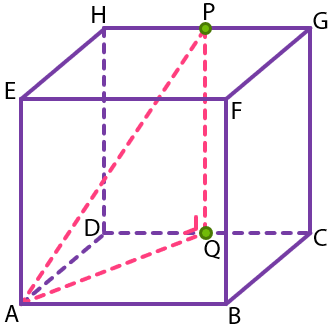
KarenaP adalah titik pada HG sehingga , maka dapat diketahui bahwa titik P adalah titik tengah HG. Dengan demikian, didapat gambar kubus ABCD.EFGH sebagai berikut. Kemudian, akan dicari jarak antaratitik A dan titik P. Gambarkan ruas garis AP terlebih dahulu! Titik A terletak pada alas kubus.Oleh karena itu, kita gambar dulu proyeksi titik P ke alas kubusdan kita namakan titik ini titik Q. Dapat diperhatikan bahwa segitiga ADQ adalah segitiga siku-siku di titik D sehingga dengan menggunakan Teorema Pythagoras didapat hubungan sebagai berikut. Kemudian, karena PQ tegak lurus dengan alas kubus, jadi PQ tegak lurus dengan garis apa pun di alas ABCD, salah satunya adalah AQ. Jadi, PQ tegak lurus dengan AQsehingga segitiga AQP adalah segitiga siku-siku yang sudut siku-sikunya adalah pada sudut AQP. Dengan menggunakan Teorema Pythagoras, didapat hubungan sebagai berikut. Karena , maka didapat hubungan sebagai berikut. Dapat diperhatikan bahwa AD adalah rusuk kubus dengan panjang sisi . Karena QP tegak lurus ABCD, maka QP sejajar DH. Kemudian, CD sejajar GH sehingga panjang QP akan sama dengan panjang rusuk DH, yaitu . Dalam hal ini, panjang DQ juga sama dengan panjang HP. Selanjutnya,dapat diperhatikan bahwa P adalah titik pada HG sehingga sehingga panjang HP dapat dihitung sebagai berikut. Karena panjang DQ sama dengan panjang HP, maka panjang DQ adalah . Oleh karena itu, didapat perhitungan sebagai berikut. Karena panjang AP tidak mungkin negatif, maka panjang AP adalah . Jadi, jawaban yang tepat adalah D.