Iklan
Pertanyaan
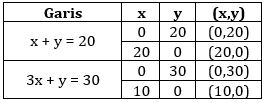
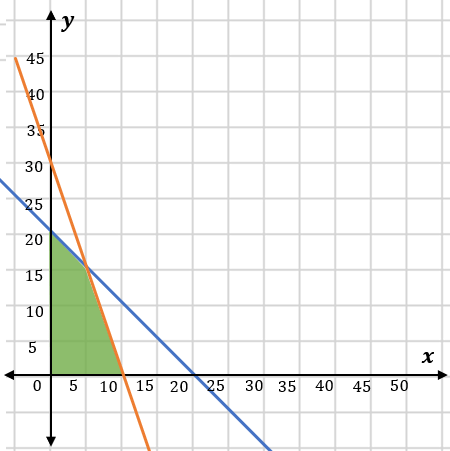
Sebuah bus dapat menampung 20 penumpang untuk diantarkan dari kota A ke kota B. Penumpang kelas bisnis dapat membawa 9 kg bagasi dan penumpang kelas ekonomi dapat membawa 3 kg bagasi. Bus tersebut hanya dapat membawa 90 kg bagasi. Jika keuntungan dari penjualan satu tiket kelas bisnis adalah Rp100.000,00 dan kelas ekonomi Rp60.000,00, maka keuntungan maksimum yang dapat diperoleh dari penjualan tiket adalah ....
Sebuah bus dapat menampung 20 penumpang untuk diantarkan dari kota A ke kota B. Penumpang kelas bisnis dapat membawa 9 kg bagasi dan penumpang kelas ekonomi dapat membawa 3 kg bagasi. Bus tersebut hanya dapat membawa 90 kg bagasi. Jika keuntungan dari penjualan satu tiket kelas bisnis adalah Rp100.000,00 dan kelas ekonomi Rp60.000,00, maka keuntungan maksimum yang dapat diperoleh dari penjualan tiket adalah ....
Rp1.000.000,00
Rp1.100.000,00
Rp1.200.000,00
Rp1.300.000,00
Rp1.400.000,00
Iklan
L. Marlina
Master Teacher
Mahasiswa/Alumni Institut Teknologi Bandung
1
0.0 (0 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia