Nilai maksimum fungsi objektif dengan kendala-kendala 2 x − 3 y ≤ 12 , x + 2 y ≤ 20 , 0 ≤ y ≤ 6 , x ≥ 2 adalah …. (UTUL UGM 2018)

Pembahasan

Pertama, kita buat dulu persamaan garis dari pertidaksamaan di atas, kemudian kita buat perpotongan garis tersebut dengan sumbu-x dan sumbu-y. Untuk garis : Saat , maka . Saat , maka . Sehingga diperoleh koordinat titik potongnya adalah dan . Untuk garis : Saat , maka . Saat , maka . Sehingga diperoleh koordinat titik potongnya adalah dan . Kemudian, karena kedua garis berpotongan di satu titik, maka untuk memperoleh koordinat titik potongnya kita eliminasi kedua persamaan tersebut. Jika kita substitusikan ke , maka diperoleh Diperoleh titik potongnya di . Perhatikan bahwa dari , kita dapat buat garis dan garis . Lalu dari pertidaksamaan , kita dapat buat persamaan garis . Selanjutnya, jika kita gambarkan garis , , , ,dan pada diagram kartesius, maka diperoleh gambar berikut ini. 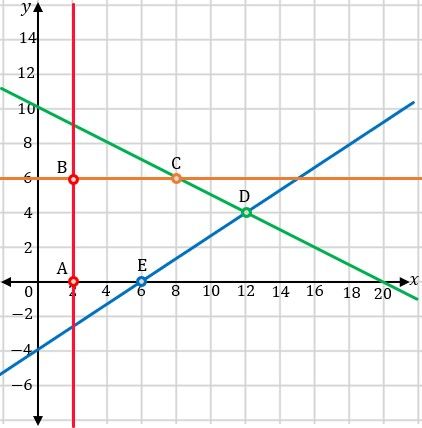Perhatikan juga dan memiliki koefisien positif dan tanda pertidaksamaannya , sehingga daerah himpunan penyelesaiannya terletak di sebelah kiri gambar garisnya. Sedangkan untuk , daerah himpunan penyelesaiannya terletak di antara dan . Terakhir, untuk , daerah himpunan penyelesaiannya terletak di sebelah kanan gambar garis . Dengan demikian, kita peroleh dearah himpunan penyelesaian yang memenuhi keempat pertidaksamaan tersebut adalah sebagai berikut. 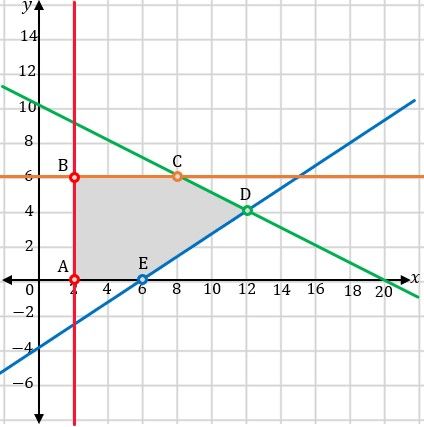Dari gambar dan perhitungan sebelumnya diperoleh koordinat A,B, C, D, dan E di atas yaitu , , , , dan . Pada soal diketahui fungsi objektinya adalah , maka kita cek dari setiap titik potok tersebut mana yang memberikan nilai maksimum. Diperoleh nilai maksimum dari pertidaksamaan di atas adalah . Jadi, jawaban yang tepat adalah D.