Nilai maksimum dari 2 x + 6 y yang memenuhi kendala-kendala − x + 4 y ≥ 1 , − 2 x + y ≥ − 12 , x + y ≥ 4 , 1 ≤ y ≤ 3 , x ≥ 0 adalah …. (UTUL UGM 2017)

Pembahasan

Pertama, kita buat dulu persamaan garis dari pertidaksamaan di atas, kemudian kita buat perpotongan garis tersebut dengan sumbu-x dan sumbu-y. Untuk garis : Saat , maka . Saat , maka . Sehingga diperoleh koordinat titik potongnya adalah dan . Untuk garis : Saat , maka . Saat , maka . Sehingga diperoleh koordinat titik potongnya adalah dan . Untuk garis : Saat , maka . Saat , maka . Sehingga diperoleh koordinat titik potongnya adalah dan . Perhatikan bahwa dari , kita dapat buat persamaan garis dan . Lalu dari pertidaksamaan , kita dapat buat persamaan garis . 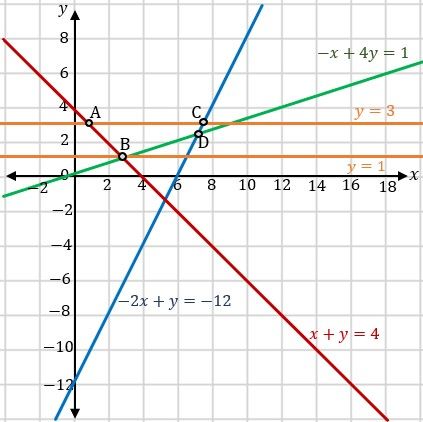Perhatikan juga , , dan memiliki koefisien positif dan tanda pertidaksamaannya , sehingga daerah himpunan penyelesaiannya terletak di atasgambar garisnya. Sedangkan untuk , daerah himpunan penyelesaiannya terletak di antara dan . Terakhir untuk , daerah himpunan penyelesaiannya terletak di sebelah kanan sumbu-y. 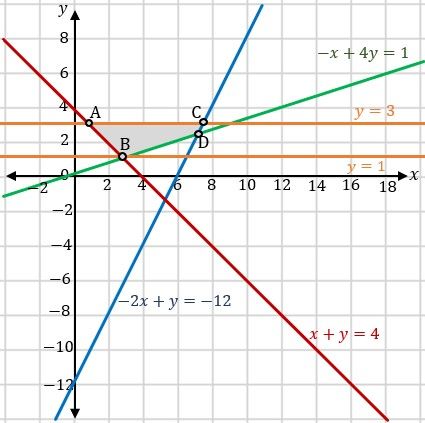Dengan demikian, kita peroleh dearah himpunan penyelesaian yang memenuhi keempat pertidaksamaan tersebut adalah Untuk memperoleh koordinat titik A,kita substitusi ke persamaan , sehingga Diperoleh koordinat titik . Untuk memperoleh koordinat B, substitusi ke persamaan . Diperoleh koordinat titik . Untuk memperoleh koordinat titik C, substitusi ke . Diperoleh koordinat titik . Untuk memperoleh koordinat titik D, eliminasi persamaan dan . Substitusi ke persamaan . Diperoleh koordinat titik . Pada soal diketahui fungsi objektinya adalah , maka kita cek dari setiap titik potok tersebut mana yang memberikan nilai maksimum. Diperoleh nilai maksimum dari pertidaksamaan di atas adalah . Jadi, jawaban yang tepat adalah D.