Ingat kembali pertidaksamaan rasional berikut.
Bentuk umum pertidaksamaan rasional adalah  dengan
dengan  .
.
Pasangan pertidaksamaan rasional akan senilai jika memiliki penyelesaian yang sama.
Perhatikan pertidaksamaan berikut.

Sehingga gambar garis bilangannya adalah
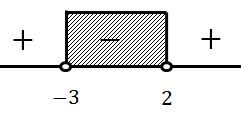
Jadi penyelesaiannya adalah  .
.
Perhatikan pertidaksamaan pada opsi A.

Sehingga gambar garis bilangannya adalah

Jadi penyelesaiannya adalah  .
.
Perhatikan pertidaksamaan pada opsi B.

Sehingga gambar garis bilangannya adalah
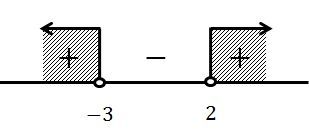
Jadi penyelesaiannya adalah  .
.
Perhatikan pertidaksamaan pada opsi C.

Karena angka pembuat nol pada opsi C berbeda dengan angka pembuat nol pada pertidaksamaan  , maka pertidaksamaan tersebut tidak senilai.
, maka pertidaksamaan tersebut tidak senilai.
Perhatikan pertidaksamaan pada opsi D.

Karena angka pembuat nol pada opsi D berbeda dengan angka pembuat nol pada pertidaksamaan  , maka pertidaksamaan tersebut tidak senilai.
, maka pertidaksamaan tersebut tidak senilai.
Perhatikan opsi E.
Opsi E merupakan persamaan, sedangkan yang diketahui adalah sebuah pertidaksamaan. Penyelesaian dari persamaan adalah sebuah angka, tetapi penyelesaian dari pertidaksamaan adalah suatu rentang, maka penyelesaiannya tidak mungkin sama. Sehingga pertidaksamaan  dan opsi E tidak senilai.
dan opsi E tidak senilai.
Pertidaksamaan  memiliki penyelesaian yang sama dengan pertidaksamaan
memiliki penyelesaian yang sama dengan pertidaksamaan  .
.
Oleh karena itu, jawaban yang benar adalah A.

















