Iklan
Pertanyaan
Perhatikan pola persegi berikut. Sebuah persegi yang lebih kecil diletakkan dalam sebuah persegi yang lebih besar dengan masing-masing titik sudutnya terletak tepat di tengah sisi dari persegi yang lebih besar. Jika luas persegi yang paling besar adalah 144 cm 2 , maka berapakah luas daerah yang diarsir pada pola ke-5? .
Perhatikan pola persegi berikut. Sebuah persegi yang lebih kecil diletakkan dalam sebuah persegi yang lebih besar dengan masing-masing titik sudutnya terletak tepat di tengah sisi dari persegi yang lebih besar.
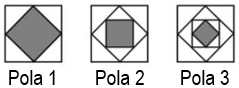
Jika luas persegi yang paling besar adalah 144 , maka berapakah luas daerah yang diarsir pada pola ke-5?.
Iklan
IR
I. Ridha
Master Teacher
Mahasiswa/Alumni Universitas Negeri Surabaya
Jawaban terverifikasi
7
5.0 (3 rating)
RA
Revany Anggraini
Ini yang aku cari! Bantu banget Makasih ❤️
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia















