Iklan

Pertanyaan

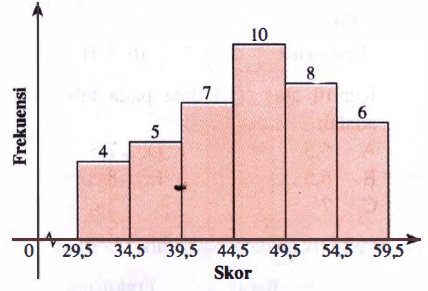
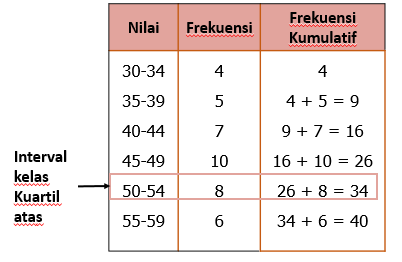
Perhatikan histogram berikut. Kuartil atas ( Q 3 ) dari data yang disajikan dalam bentukhistogramtersebut adalah ....

Perhatikan histogram berikut.

Kuartil atas $(Q_{3})$ dari data yang disajikan dalam bentuk histogram tersebut adalah ....

$51, 5$
$52, 0$
$52, 5$
$53, 0$
$53, 5$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

02

:

07

:

31

:

57

Iklan

MM

M. Mariyam

Master Teacher

Mahasiswa/Alumni Institut Pertanian Bogor

Jawaban terverifikasi

Pembahasan

Ingat kembali rumus kuartil atas pada data berkelompok sebagai berikut: Q 3 = L 3 + c ⎝ ⎛ f 3 4 3 n − F 3 ⎠ ⎞ dimana Q 3 = kuartil atas L 3 = tepi bawah kelas kuartil atas n = ukuran data (jumlah frekuensi) f 3 = frekuensi pada interval kelas kuartil atas F 3 = frekuensi kumulatif sebelum kelas kuartil atas c = panjang kelas Oleh karena itu, berdasarkan histogram di atas dapat dibuattabel distribusi frekuensi sebagai berikut: Interval kelas kuartil atas terletak pada 50 − 54 diperoleh dari 4 3 n = 4 3 × 40 = 30 (lihat kolom frekuensi kumulatif) dengan n = 40 , L 3 = 50 − 0 , 5 = 49 , 5 , f 3 = 8 , F 3 = 26 , c = 5 Q 3 = = = = = L 3 + c ⎝ ⎛ f 3 4 3 n − F 3 ⎠ ⎞ 49 , 5 + 5 ⋅ ⎝ ⎛ 8 4 3 ⋅ 40 − 26 ⎠ ⎞ 49 , 5 + 5 ⋅ ( 8 30 − 26 ) 49.5 + 2 , 5 52 , 0 Dengan demikian, kuartil atas data tersebut adalah 52 , 0 . Jadi, pilihan jawaban yang tepat adalah B.

Ingat kembali rumus kuartil atas pada data berkelompok sebagai berikut:

$Q_{3} = L_{3} + c ⎝ ⎛ \frac{\frac{3}{4} n - F _{3}}{f _{3}} ⎠ ⎞$

dimana

$Q_{3} =$ kuartil atas

$L_{3} =$ tepi bawah kelas kuartil atas

$n =$ ukuran data (jumlah frekuensi)

$f_{3} =$ frekuensi pada interval kelas kuartil atas

$F_{3} =$ frekuensi kumulatif sebelum kelas kuartil atas

$c =$ panjang kelas

Oleh karena itu, berdasarkan histogram di atas dapat dibuat tabel distribusi frekuensi sebagai berikut:

Interval kelas kuartil atas terletak pada $50 - 54$ diperoleh dari $\frac{3}{4} n = \frac{3}{4} \times 40 = 30$ (lihat kolom frekuensi kumulatif) dengan

$n = 40, L_{3} = 50 - 0, 5 = 49, 5, f_{3} = 8, F_{3} = 26, c = 5$

$Q_{3} = = = = = L_{3} + c ⎝ ⎛ \frac{\frac{3}{4} n - F _{3}}{f _{3}} ⎠ ⎞ 49, 5 + 5 \cdot ⎝ ⎛ \frac{\frac{3}{4} \cdot 40 - 26}{8} ⎠ ⎞ 49, 5 + 5 \cdot (\frac{30 - 26}{8}) 49.5 + 2, 5 52, 0$

Dengan demikian, kuartil atas data tersebut adalah $52, 0$ .

Jadi, pilihan jawaban yang tepat adalah B.

Buka akses jawaban yang telah terverifikasi

lock

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

21

4.3 (3 rating)

Iklan

Pertanyaan serupa

Tentukan kuartil pertama, kuartil kedua, dan kuartil ketiga dari data pada histogram di samping!

32

4.4

Jawaban terverifikasi

Tentukan median dan kuartil dari data yang dinyatakan dengan histogram berikut.

21

5.0

Jawaban terverifikasi

Iklan

Tentukan hamparan dari data yang disajikan dalam bentuk histogram di samping!

4

5.0

Jawaban terverifikasi

Tentukan nilai kuartil ketiga dari data pada histogram di samping!

4

4.4

Jawaban terverifikasi

Tentukan hamparan dan simpangan kuartildari data yang disajikan dalam bentuk histogram di samping!

23

3.6

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

RUANGGURU HQ

Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860

Coba GRATIS Aplikasi Roboguru

Download di Google Play

Coba GRATIS Aplikasi Ruangguru

Download di Google Play

Download di Appstore

Download di App Gallery

Produk Ruangguru

Produk Lainnya

Bantuan & Panduan

Hubungi Kami

+62 815-7441-0000

Email info@ruangguru.com

info@ruangguru.com

Contact 02130930000

02130930000

Ikuti Kami

Instagram Roboguru

Youtube Ruangguru

©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia