Iklan
Pertanyaan
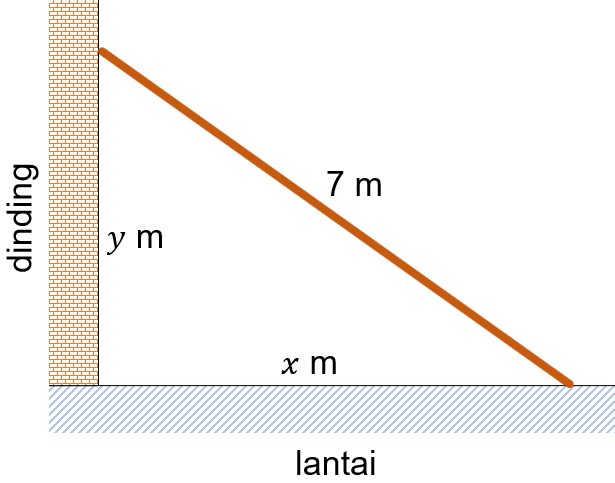
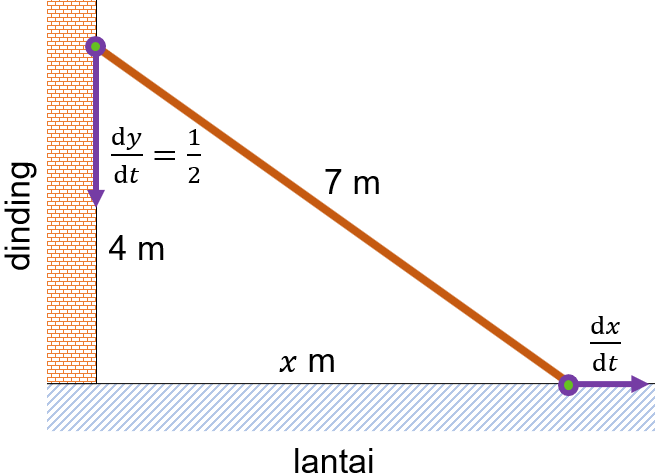
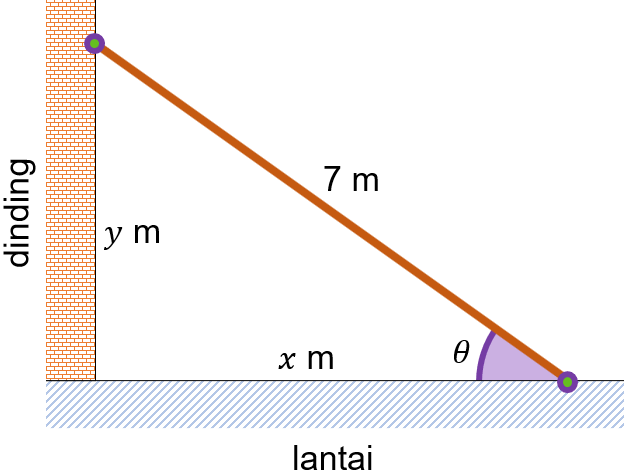
Perhatikan gambar di bawah ini! Sebuah tangga dengan panjang 7 meter disandarkan pada sebuah dinding. Karena tangga ditempatkan pada sebuah lantai yang licin, tangga tersebut merosot sehingga pada saat jarak puncak tangga dengan lantai adalah 4 meter, posisi ujung tangga yang menempel dengan dinding bergeser dengan perubahan laju posisi 2 1 m / s ke bawah. Pada saat tersebut, kondisi yang terjadi terkait laju perubahan pada ujung tangga yang menempel pada lantai dan lanju perubahan pada besar sudut antara tangga dan lantai adalah ....
Perhatikan gambar di bawah ini!
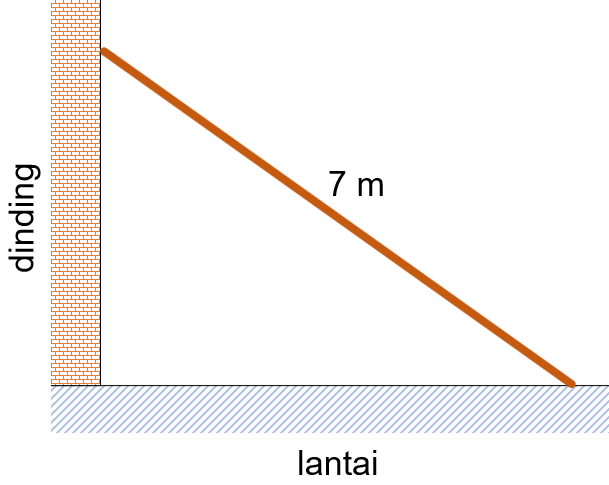
Sebuah tangga dengan panjang 7 meter disandarkan pada sebuah dinding. Karena tangga ditempatkan pada sebuah lantai yang licin, tangga tersebut merosot sehingga pada saat jarak puncak tangga dengan lantai adalah 4 meter, posisi ujung tangga yang menempel dengan dinding bergeser dengan perubahan laju posisi ke bawah. Pada saat tersebut, kondisi yang terjadi terkait laju perubahan pada ujung tangga yang menempel pada lantai dan lanju perubahan pada besar sudut antara tangga dan lantai adalah ....
ujung tangga yang menempel pada lantai menjauhi dinding dengan laju dan terjadi pengurangan besar sudut dengan laju
ujung tangga yang menempel pada lantai menjauhi dinding dengan laju dan terjadi penambahan besar sudut dengan laju
ujung tangga yang menempel pada lantai mendekati dinding dengan laju dan terjadi pengurangan besar sudut dengan laju
ujung tangga yang menempel pada lantai menjauhi dinding dengan laju dan terjadi pengurangan besar sudut dengan laju
ujung tangga yang menempel pada lantai menjauhi dinding dengan laju dan terjadi penambahan besar sudut dengan laju
Iklan
R. Rohmat
Master Teacher
2
0.0 (0 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia