Pertanyaan

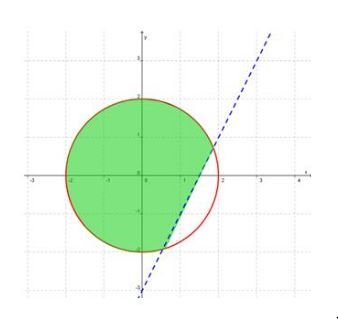
Perhatikan gambar berikut ini. Daerah yang diarsir menyatakan daerah himpunan penyelesaian suatu sistem pertidaksamaan kuadrat dua variabel. Sistem pertidaksamaan yang sesuai untuk gambar tersebut adalah ....

Perhatikan gambar berikut ini.

Daerah yang diarsir menyatakan daerah himpunan penyelesaian suatu sistem pertidaksamaan kuadrat dua variabel. Sistem pertidaksamaan yang sesuai untuk gambar tersebut adalah .... $\;$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

E. Nur

Master Teacher

Mahasiswa/Alumni Institut Teknologi Sepuluh Nopember

Jawaban terverifikasi

Pembahasan

Daerah yang diarsir dibatasi oleh sebuah lingkaran dan sebuah garis lurus. Persamaan lingkaran dengan adalah Persamaan garis lurus yang melalui titik dan adalah Uji titik dalam arsiran untuk menentukan tanda pertidaksamaannya. Ambil titik . ( i ) sehingga . ( ii ) sehingga . Dengan demikian sistem pertidaksamaan dari garis yang diarsir adalah .

Daerah yang diarsir dibatasi oleh sebuah lingkaran dan sebuah garis lurus.

Persamaan lingkaran dengan jari minus jari space open parentheses straight r close parentheses equals 2 space satuan space dan space pusat space open parentheses 0 comma 0 close parentheses adalah

table attributes columnalign right center left columnspacing 0px end attributes row cell x squared plus y squared end cell equals cell 2 squared end cell row cell x squared plus y squared end cell equals cell 4 space.... open parentheses straight i close parentheses end cell end table

Persamaan garis lurus yang melalui titik open parentheses 0 comma 3 close parentheses dan open parentheses 2 comma 1 close parentheses adalah

$table attributes columnalign right center left columnspacing 0px end attributes row cell fraction numerator y minus y subscript 1 over denominator y subscript 2 minus y subscript 1 end fraction end cell equals cell fraction numerator x minus x subscript 1 over denominator x subscript 2 minus x subscript 1 end fraction end cell row cell fraction numerator y plus 3 over denominator 1 plus 3 end fraction end cell equals cell fraction numerator x minus 0 over denominator 2 minus 0 end fraction end cell row cell fraction numerator y plus 3 over denominator 4 end fraction end cell equals cell x over 2 end cell row cell 2 open parentheses y plus 3 close parentheses end cell equals cell 4 x end cell row cell 2 y plus 6 end cell equals cell 4 x end cell row cell negative 4 x plus 2 y end cell equals cell negative 6 end cell row cell 2 x minus y end cell equals 3 end table$

Uji titik dalam arsiran untuk menentukan tanda pertidaksamaannya. Ambil titik open parentheses 0 comma 0 close parentheses .

( i ) x squared plus y squared equals 0 squared plus 0 squared equals 0 less or equal than 4 sehingga x squared plus y squared less or equal than 4 .

( ii ) 2 x minus y equals 2 open parentheses 0 close parentheses minus 0 equals 0 less or equal than 3 sehingga 2 x minus y less or equal than 3 .

Dengan demikian sistem pertidaksamaan dari garis yang diarsir adalah

open curly brackets table attributes columnalign left end attributes row cell x squared plus y squared less or equal than 4 end cell row cell 2 x minus y less or equal than 3 end cell end table close .