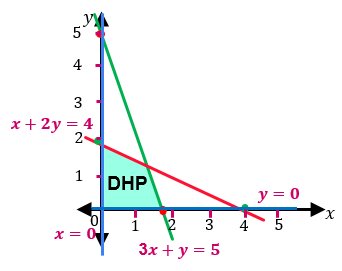
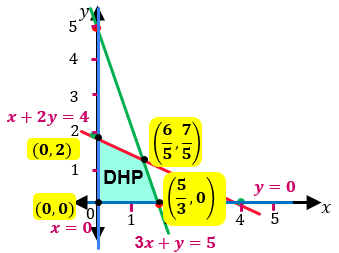
Pemerintah Kabupaten Majene akan mengirim bantuan berupa makanan, pakaian dan lain-lain ke gempa bumi dan tsunami di Palu. Untuk mengangkut bantuan tersebut tersedia dua jenis mobil angkutan barang. Mobil jenis A dapat mengangkut 30 karung beras dan 50 dus air mineral, sedangkan mobil jenis B dapat mengangkut 10 karung beras dan 100 dus air mineral. Pemerintah akan mengirim 50 karung beras dan 200 dus air mineral. Jika sewa mobil jenis A sebesar Rp400.000,00 dan sewa mobil jenis B sebesar Rp800.000,00. Berapa pengeluaranminimum untuk mengangkut barang tersebut adalah ....

Pembahasan

Terlebih dahulu buatlah model matematika dari permasalahan di atas. Misalkan: banyaknya mobil jenis A adalah , dan banyaknyamobil jenis B adalah . Berikut ini sistem pertidaksamaan yang diperoleh dari tabel diatas: Banyaknya mobil A dan B tidak mungkin negatif, sehigga x ≥ 0 y ≥ 0 Karena sewa mobil jenis A sebesar Rp400.000,00 dan sewa mobil jenis B sebesar Rp800.000,00 maka fungsi objektif pengeluaran dari permasalahan tersebut adalah: Akan digambarkan grafik garis pada SPtLDV di atas ke dalam koordinat kartesius. Untuk menggambar grafik garisnya,cukup dengan menentukan titik potong sumbu-X dan sumbu-Y sehingga dapat tarik garis dari dua titik potong tersebut. Titik potong sumbu-X dan sumbu Y pada persamaan 3 x + y = 5 dengan menggunakan tabel diperoleh: x 0 3 5 ​ y 5 0 diperoleh titik potong ( 0 , 5 ) dan ( 3 5 ​ , 0 ) . Titik potong sumbu-X dan sumbu Y pada persamaan x + 2 y = 4 dengan menggunakan tabel diperoleh: x 0 4 y 2 0 diperoleh titik potong ( 0 , 2 ) dan ( 4 , 0 ) . Gambar grafik garis dariSPtLDV di atas diperoleh sebagai berikut: Gunakan titik pojok daerah himpunan penyelesaian untuk menentukan pengeluaran minimum untuk mengangkut barang tersebut, sehingga harus dicari terlebih dahulu titik potong antara dua garis tersebut diperoleh dengan mengubah pertidaksamaan menjadi persamaan kemudian gunakan eliminasi-substitusiseperti berikut: Diperoleh nilai , substitusikan ke salah satu persamaan diperoleh: Diperoleh nilai , maka titik potong kedua grafik tersebut adalah . Titik pojok dari daerah penyelesaian adalah , , , dan . Seperti gambar grafik berikut ini. Karena banyaknya kedua mobil tidak boleh 0 dan tidak mungkin bernilai pecahan, maka diperoleh titiknya adalah ( 0 , 2 ) , sehingga pengeluaran minimumnya dapat dihitung sebagai berikut. Sehingga diperoleh pada titik ( 0 , 2 ) nilai minimumnya adalah 1.600.000, sehingga dengan hanya menyewa mobil jenis B sebanyak 2 unit akan diperoleh pengeluaran minimum sebesar Rp1.600.000.