Pertanyaan

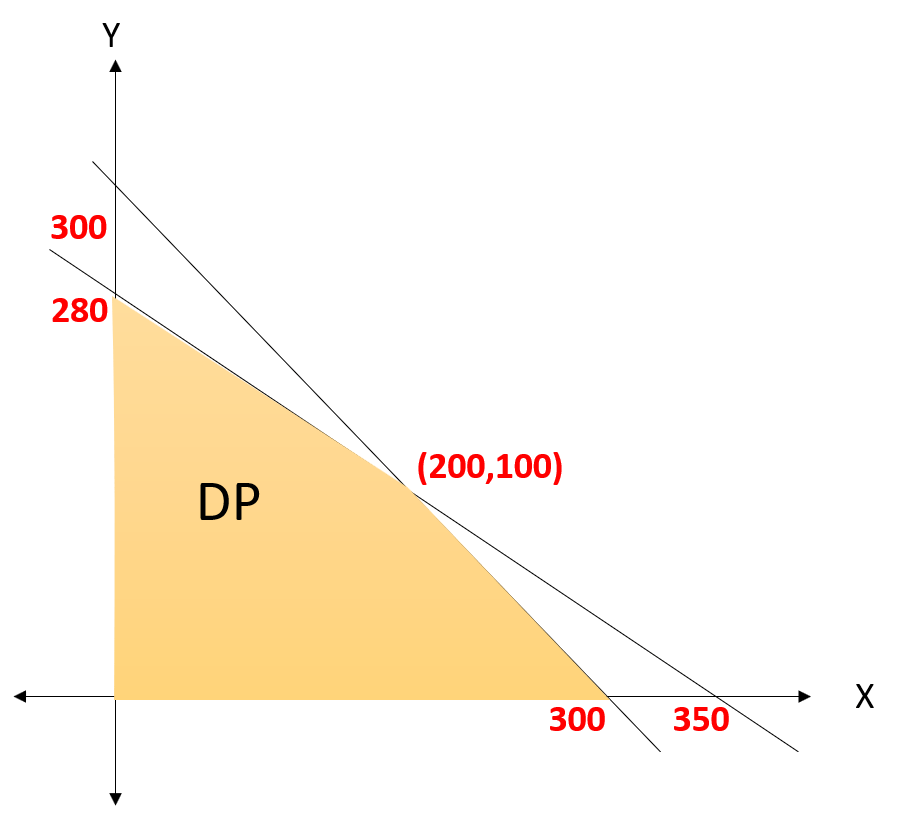
Pak Dandi membeli es krim. Jenis I dengan harga Rp 500,- dan jenis II dengan harga Rp 400,-. Lemari es Pak Dandi hanya dapat menampung tidak lebih dari 300 buah dan uang yang dipunya Pak Dandi hanya Rp 140.000,-. Jika es krim tersebut dijual kembali dengan untung Rp 100,- perbuah, maka banyak es krim jenis I dan II yang harus dibeli jika terjual seluruhnya untuk mendapatkan keuntungan sebesar-besarnya.

Pak Dandi membeli es krim. Jenis I dengan harga Rp 500,- dan jenis II dengan harga Rp 400,-. Lemari es Pak Dandi hanya dapat menampung tidak lebih dari $300$ buah dan uang yang dipunya Pak Dandi hanya Rp 140.000,-. Jika es krim tersebut dijual kembali dengan untung Rp 100,- perbuah, maka banyak es krim jenis I dan II yang harus dibeli jika terjual seluruhnya untuk mendapatkan keuntungan sebesar-besarnya.

M. Mariyam

Master Teacher

Mahasiswa/Alumni Institut Pertanian Bogor

Jawaban terverifikasi

Jawaban

keuntungan maksimum yang diperoleh Pak Daud adalah Rp30.000,00 dengan menjual 200 es krim jenis I dan 100 es krim jenis II atau 300 es krim jenis I saja.

keuntungan maksimum yang diperoleh Pak Daud adalah Rp30.000,00 dengan menjual 200 es krim jenis I dan 100 es krim jenis II atau 300 es krim jenis I saja.

Pembahasan

Misalkan x = es krim jenis I dan y = es krim jenis II, model matematika dari permasalahan di atas adalah Fungsi objektif : Kendala : membuat gambar daerah penyelesaian dari sistem pertidaksamaan berikut : Titik potong kedua garis, sebagai berikut: Kita substitusikan titik-titik tersebut ke fungsi objektif (0, 280) ⇒ f = 100(0) + 100(280) = 28.000 (200, 100) ⇒ f = 100(200) + 100(100) = 30.000 (300, 0) ⇒ f = 100(300) + 100(0) = 30.000 Jadi keuntungan maksimum yang diperoleh Pak Daud adalah Rp30.000,00 dengan menjual 200 es krim jenis I dan 100 es krim jenis II atau 300 es krim jenis I saja.

Misalkan x = es krim jenis I dan y = es krim jenis II, model matematika dari permasalahan di atas adalah

Fungsi objektif :

Kendala :

membuat gambar daerah penyelesaian dari sistem pertidaksamaan berikut :

Titik potong kedua garis, sebagai berikut:

begin mathsize 14px style 5 x plus 4 y equals 1.400 space space x plus space space y equals space space space space 300 open parentheses persamaan space dikali space 4 close parentheses vertical ellipsis vertical ellipsis 5 x plus 4 y equals 1.400 bottom enclose 4 x plus 4 y equals 1.200 space minus end enclose space x equals 200 space y equals 100 end style

Kita substitusikan titik-titik tersebut ke fungsi objektif

(0, 280) ⇒ f = 100(0) + 100(280) = 28.000
(200, 100) ⇒ f = 100(200) + 100(100) = 30.000
(300, 0) ⇒ f = 100(300) + 100(0) = 30.000

Jadi keuntungan maksimum yang diperoleh Pak Daud adalah Rp30.000,00 dengan menjual 200 es krim jenis I dan 100 es krim jenis II atau 300 es krim jenis I saja.

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

5.0 (5 rating)

Pertanyaan serupa

Suatu perusahaan transportasi harus mendistribusikan 1.200 paket (yang besarnya sama) melalui dua truk pengangkut. Truk 1 memuat 200 paket untuk setiap pengangkutan dan truk 2 memuat 80 paket untuk se...

4.5

Jawaban terverifikasi

PT Usaha Rotanindo di Cirebonmemproduksi dua jenis mebel rotan, yaitujenis kursi dan meja. Kapasitas produksiperusahaan tidak kurang dari 1.000 unitbarang per bulan. Dari bagian marketing,diperoleh in...

5.0

Jawaban terverifikasi

Seorang pemborong mempunyaipersediaan 100 kaleng cat warna hijaudan 240 kaleng cat warna abu-abu.Pemborong tersebut mendapat order untuk mengecat ruang tamu dan ruang tidur disuatu gedung. Setelah dik...

3.0

Jawaban terverifikasi

Seorang pedagang ponsel memilikimodal sebesar Rp 49.600.000 , 00 untukmenjual dua jenis ponsel sebanyak-banyaknya 25 unit. Pedagang tersebutakan menjual ponsel jenis android danjenis biasa dengan harg...

4.7

Jawaban terverifikasi

Harga bawang merah Rp 25.000,00 per kg dan harga bawang putih Rp 50.000,00 per kg. Seorang pedangan hanya mempunyai modal Rp 20.000.000,00 dan kiosnnya hanya dapat memuat tidak lebih dari 600 kg denga...

3.0

Jawaban terverifikasi