Iklan
Pertanyaan
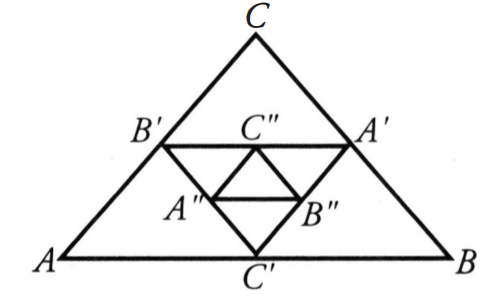
Pada segitiga sama sisi A BC yang diketahui sisi-sisinya , digambarkan titik-titik A ′ , B ′ , dan C ′ berturut-turut dengan titik tengah sisi BC , C A , dan A B sehingga menghasilkan segitiga A ′ B ′ C ′ . Proses tersebut diulangi kembali pada segitiga A ′ B ′ C ′ sehingga diperoleh segitiga A " B " C " , dan seterusnya. Jumlahluas segitiga A BC , A ′ B ′ C ′ , A " B " C " , ... dan seterusnya adalah ....
Pada segitiga sama sisi yang diketahui sisi-sisinya , digambarkan titik-titik , , dan berturut-turut dengan titik tengah sisi , , dan sehingga menghasilkan segitiga .
Proses tersebut diulangi kembali pada segitiga sehingga diperoleh segitiga , dan seterusnya. Jumlah luas segitiga , , , ... dan seterusnya adalah ....
Iklan
HE
H. Eka
Master Teacher
Mahasiswa/Alumni Universitas Pendidikan Indonesia
Jawaban terverifikasi
5
5.0 (1 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2025 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia