Iklan
Pertanyaan
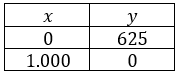
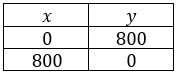
Pada masa pandemi Covid- 19 ini Pemerintah memberikan bantuan tunai untuk masyarakat yang terkena dampak dengan memberikan dana bantuan Usaha Kecil sebesar Rp 2.500.000 , 00 . Pak Anda adalah salah satu penerima dana bantuan menggunakan uang yang diterimanya untuk berjualan minuman segar yaitu jus jeruk dalam kemasan botol ukuran 150 ml dan 250 ml . Untuk yang ukuran perbotol memerlukan biaya produksi Rp 2.500 , 00 dan dijual Rp 4.000 , 00 , sedangkan untuk yang ukuran perbotol memerlukan biaya produksi sebesar dan dijual Rp 6.000 , 00 . Jika wadah untuk penyimpanan jus jeruk tersebut yang akan dijual mampu menyimpan paling banyak 800 botol, maka keuntungan maksimum yang akan diperoleh Pak Anda apabila semua minumannya habis terjual adalah... .
Pada masa pandemi Covid- ini Pemerintah memberikan bantuan tunai untuk masyarakat yang terkena dampak dengan memberikan dana bantuan Usaha Kecil sebesar . Pak Anda adalah salah satu penerima dana bantuan menggunakan uang yang diterimanya untuk berjualan minuman segar yaitu jus jeruk dalam kemasan botol ukuran dan . Untuk yang ukuran perbotol memerlukan biaya produksi dan dijual , sedangkan untuk yang ukuran
perbotol memerlukan biaya produksi sebesar
dan dijual . Jika wadah untuk penyimpanan jus jeruk tersebut yang akan dijual mampu menyimpan paling banyak botol, maka keuntungan maksimum yang akan diperoleh Pak Anda apabila semua minumannya habis terjual adalah... .
Iklan
A. Allamah
Master Teacher
Mahasiswa/Alumni Universitas Brawijaya
1
0.0 (0 rating)
Iklan
Pertanyaan serupa
RUANGGURU HQ
Jl. Dr. Saharjo No.161, Manggarai Selatan, Tebet, Kota Jakarta Selatan, Daerah Khusus Ibukota Jakarta 12860
Produk Ruangguru
Bantuan & Panduan
Hubungi Kami
©2026 Ruangguru. All Rights Reserved PT. Ruang Raya Indonesia