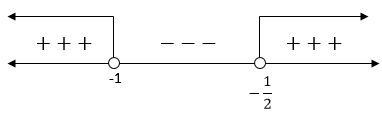Nilai-nilai x yang memenuhi 3 − 3 x + 3 x 2 − 3 x 3 + ... < 6 adalah ....

Pembahasan

Jawaban yang benar untuk pertanyaan tersebut adalah C. Ingat rumus deret geometri tak hingga: S n ​ ​ = ​ 1 − r a ​ ​ , dengan − 1 < r < 1 Keterangan: S n ​ : jumlahderetgeometritakhingga a : sukupertamaderetgeometritakhingga r : rasiogeometritakhingg Diketahui: 3 − 3 x + 3 x 2 − 3 x 3 + ... < 6 Barisan 3 − 3 x + 3 x 2 − 3 x 3 + ... < 6 ↔ 1 − x + x 2 − x 3 + ... < 2 . Barisan di atas merupakan deret geometri tak hingga dengan rasio: r = u 1 ​ u 2 ​ ​ = 1 − x ​ = − x Syarat rasio deret geometri tak hingga yaitu: − 1 ​ < ↔ ↔ ​ r < 1 − 1 < − x < 1 − 1 < x < 1 ​ Jumlah deret geometri tak hingga dari deret tersebut yaitu: S n ​ 1 − ( − x ) 1 ​ 1 + x 1 ​ 1 + x 1 ​ − 2 1 + x 1 − 2 ( 1 + x ) ​ 1 + x 1 − 2 − 2 x ​ 1 + x − 1 − 2 x ​ 1 + x − 2 x − 1 ​ 1 + x 2 x + 1 ​ ​ = < < < < < < < > ​ 1 − r a ​ 2 2 0 0 0 0 0 ​ Pembuat nol dari pertidaksamaan rasional di atas: Pembilang: 2 x + 1 = 0 → 2 x = − 1 → x = − 2 1 ​ Penyebut: 1 + x = 0 → x = − 1 Perlu diingat bahwa penyebut bernilai tidak sama dengan nol sehingga bulatan pada garis bilangan adalah bulatan kosong. Mencari daerah positif dan negatif dengan melakukan titik uji. Misalkan substitusikan x = 0 ke persamaan ​ ​ 1 + x 2 x + 1 ​ ​ ternyata menghasilkan bilangan positif maka daerah di sebelah kanan titik − 2 1 ​ merupakan daerah positif. 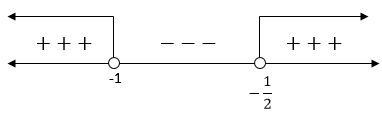Sehingga garis bilangannya: Himpunan penyelesaiannya: { x ∣ x < − 1 atau x > − 2 1 ​ } . Karena syarat rasio deret geometri − 1 ​ < ​ x < 1 ​ , maka himpunan penyelesaian yang memenuhi yaitu irisan dari ​ ​ { x ∣ − 1 < x < 1 } ​ dan { x ∣ x < − 1 atau x > − 2 1 ​ } yaitu − 2 1 ​ < x < 1 . Oleh karena itu, jawaban yang benar adalah C.