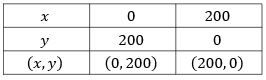
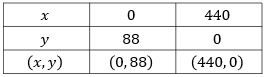
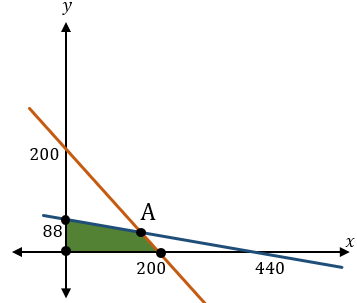
Luas sebuah parkiranmobil adalah 1.760 m 2 . Parkiran tersebut hanya dapat menampung 200 mobil. Luas parkiran untuk sebuah mobil kecil adalah 4 m 2 dan untuksebuah mobil besar adalah 20 m 2 . Biaya parkir sebuah mobil kecil adalah Rp1.000,00/jam, sedangkan biaya parkir sebuah mobil besar adalah Rp2.000,00/jam. Jika dalam 1 jam parkiran mobil tersebut terisi penuh dan tidak ada mobil yang pergi dan datang, maka biaya parkir maksimum yang didapat adalah ....

Pembahasan

Dari permasalahan pada soal, didapat permisalan sebagai berikut. : banyak mobil kecil : banyak mobil besar Diketahui bahwa luas parkirantersebut adalah dengan ketentuan luassebuah mobil kecil adalah dan untuksebuah mobil besar adalah Oleh karena itu, didapat pertidaksamaan sebagai berikut. Selanjutnya, parkiran tersebut hanya dapat menampung 200 mobil, maka didapat pertidaksamaan berikut. Kemudian, karena banyak mobil tidak mungkin negatif, maka didapat pertidaksamaan berikut. Diketahui bahwabiaya parkir sebuah mobil kecil adalah Rp1.000,00/jam dan biaya parkir sebuah mobil besar adalah Rp2.000,00/jam. Kemudian,dalam 1 jam terisi penuh dan tidak ada mobil yang pergi dan datang. Oleh karena itu, fungsi objektifnya adalah sebagai berikut. Langkah selanjutnya adalah gambardaerah penyelesaian dari sistem pertidaksamaan di atas. Terlebih dahulu, akan dicari titik potong garis terhadap sumbu- dan sumbu- Selanjutnya, akan dicarititik potong garis terhadapsumbu- dan sumbu- Oleh karena itu, didapat daerah penyelesaiannya seperti gambar berikut ini. MisalA adalah titik potong kedua garis, koordinat titik A dapat dicari sebagai berikut. Kemudian, substitusi ke persamaan sebagai berikut. Didapat bahwa koordinat A adalah Kemudian, substitusikan masing-masing titik pojok ke fungsi objektif untuk mencari nilai maksimumnya. Dengan demikian, penghasilan maksimum dalam 1 jam tersebutadalah Rp260.000,00. Jadi, jawaban yang tepat adalah C.