Pertanyaan

Jika 0 ≤ x ≤ 4 , maka nilai x yang memenuhi persamaan cos ( 3 π x ) ⋅ cos ( 2 π x ) ≤ 0 adalah . . .

Jika $0 \leq x \leq 4$ , maka nilai $x$ yang memenuhi persamaan $cos (\frac{π}{3} x) \cdot cos (\frac{π}{2} x) \leq 0$ adalah . . .

$1 \leq x \leq \frac{3}{2} atau 3 \leq x \leq 4$
$1 \leq x \leq \frac{3}{2} atau 2 \leq x \leq 4$
$1 \leq x \leq \frac{3}{2} atau 2 \leq x \leq 3$
$1 \leq x \leq \frac{3}{2} atau 2 \leq x \leq \frac{5}{2}$
$1 \leq x \leq 2 atau 3 \leq x \leq 4$

A. Salim

Master Teacher

Mahasiswa/Alumni Universitas Pelita Harapan

Jawaban terverifikasi

Jawaban

jawaban yang tepat adalah A

Pembahasan

Ingat bahwa : Sudut berelasi cos ( π − α ) = − cos α cos ( π + α ) = − cos α cos ( 2 π − α ) = cos α dari soal diketahui cos ( 3 π x ) ⋅ cos ( 2 π x ) ≤ 0 ↔ cos ( 3 π x ) = 0 atau cos ( 2 π x ) = 0 Sehingga 1. Untuk cos ( 3 π x ) = 0 berlaku cos ( 3 π x ) cos ( 3 π x ) 3 π x x = = = = 0 cos 2 π atau cos ( 3 π x ) = cos 2 3 π 2 π atau 3 π x = 2 3 π 2 3 atau x = 2 9 karena 0 ≤ x ≤ 4 , maka x yang memenuhi adalah x = 2 3 . 2. Untuk cos ( 2 π x ) = 0 berlaku cos ( 2 π x ) cos ( 2 π x ) 2 π x x = = = = 0 cos 2 π atau cos ( 2 π x ) = cos 2 3 π 2 π atau 2 π x = 2 3 π 1 atau x = 3 karena 0 ≤ x ≤ 4 , maka x yang memenuhi adalah x = 1 dan x = 3 . Oleh karena itu, kita telah memiliki 5 titik kritis, yaitu x = 0 , 1 , 2 3 , 3 , 4. Selanjutnya kita lakukan uji titik sebagai berikut. Daerah 0 ≤ x ≤ 1 , ambil x = 2 1 diperoleh cos ( 3 π ⋅ 2 1 ) ⋅ cos ( 2 π ⋅ 2 1 ) = = cos 6 π ⋅ cos 4 π + ⋅ + > 0 . Daerah 1 ≤ x ≤ 2 3 , ambil x = 4 5 diperoleh cos ( 3 π ⋅ 4 5 ) ⋅ cos ( 2 π ⋅ 4 5 ) = = cos 12 5 π ⋅ cos 8 5 π + ⋅ − < 0 . Daerah 2 3 ≤ x ≤ 3 , ambil x = 2 diperoleh cos ( 3 π ⋅ 2 ) ⋅ cos ( 2 π ⋅ 2 ) = = cos 3 2 π ⋅ cos π − ⋅ − > 0 . Daerah 3 ≤ x ≤ 4 , ambil x = 2 7 diperoleh cos ( 3 π ⋅ 2 7 ) ⋅ cos ( 2 π ⋅ 2 7 ) = = cos 6 7 π ⋅ cos 4 7 π − ⋅ + < 0 . 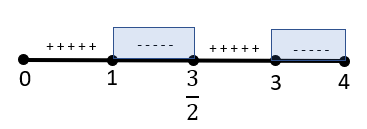Sehingga garis bilangan yang terbentuk adalah Dengan demikian,nilai x yang memenuhi persamaan cos ( 3 π x ) ⋅ cos ( 2 π x ) ≤ 0 adalah 1 ≤ x ≤ 2 3 atau 3 ≤ x ≤ 4 . Jadi, jawaban yang tepat adalah A

Ingat bahwa :

Sudut berelasi

$cos (π - α) = - cos α cos (π + α) = - cos α cos (2 π - α) = cos α$

dari soal diketahui

$cos (\frac{π}{3} x) \cdot cos (\frac{π}{2} x) \leq 0 \leftrightarrow cos (\frac{π}{3} x) = 0 atau cos (\frac{π}{2} x) = 0$

Sehingga

1. Untuk $cos (\frac{π}{3} x) = 0$ berlaku

$cos (\frac{π}{3} x) cos (\frac{π}{3} x) \frac{π}{3} x x = = = = 0 cos \frac{π}{2} atau cos (\frac{π}{3} x) = cos \frac{3 π}{2} \frac{π}{2} atau \frac{π}{3} x = \frac{3 π}{2} \frac{3}{2} atau x = \frac{9}{2}$

karena $0 \leq x \leq 4$ , maka $x$ yang memenuhi adalah $x = \frac{3}{2}$ .

2. Untuk $cos (\frac{π}{2} x) = 0$ berlaku

$cos (\frac{π}{2} x) cos (\frac{π}{2} x) \frac{π}{2} x x = = = = 0 cos \frac{π}{2} atau cos (\frac{π}{2} x) = cos \frac{3 π}{2} \frac{π}{2} atau \frac{π}{2} x = \frac{3 π}{2} 1 atau x = 3$

karena $0 \leq x \leq 4$ , maka $x$ yang memenuhi adalah $x = 1 dan x = 3$ .

Oleh karena itu, kita telah memiliki $5$ titik kritis, yaitu $x = 0, 1, \frac{3}{2}, 3, 4.$ Selanjutnya kita lakukan uji titik sebagai berikut.

Daerah $0 \leq x \leq 1, ambil x = \frac{1}{2}$ diperoleh $cos (\frac{π}{3} \cdot \frac{1}{2}) \cdot cos (\frac{π}{2} \cdot \frac{1}{2}) = = cos \frac{π}{6} \cdot cos \frac{π}{4} + \cdot + > 0$ .
Daerah $1 \leq x \leq \frac{3}{2}, ambil x = \frac{5}{4}$ diperoleh $cos (\frac{π}{3} \cdot \frac{5}{4}) \cdot cos (\frac{π}{2} \cdot \frac{5}{4}) = = cos \frac{5 π}{12} \cdot cos \frac{5 π}{8} + \cdot - < 0$ .
Daerah $\frac{3}{2} \leq x \leq 3, ambil x = 2$ diperoleh $cos (\frac{π}{3} \cdot 2) \cdot cos (\frac{π}{2} \cdot 2) = = cos \frac{2 π}{3} \cdot cos π - \cdot - > 0$ .
Daerah $3 \leq x \leq 4, ambil x = \frac{7}{2}$ diperoleh $cos (\frac{π}{3} \cdot \frac{7}{2}) \cdot cos (\frac{π}{2} \cdot \frac{7}{2}) = = cos \frac{7 π}{6} \cdot cos \frac{7 π}{4} - \cdot + < 0$ .

Sehingga garis bilangan yang terbentuk adalah

Dengan demikian, nilai $x$ yang memenuhi persamaan $cos (\frac{π}{3} x) \cdot cos (\frac{π}{2} x) \leq 0$ adalah $1 \leq x \leq \frac{3}{2} atau 3 \leq x \leq 4$ .