Gunakan konsep penyelesaian pertidaksamaan trigonometri dengan garis bilangan dan persamaan trigonometri.

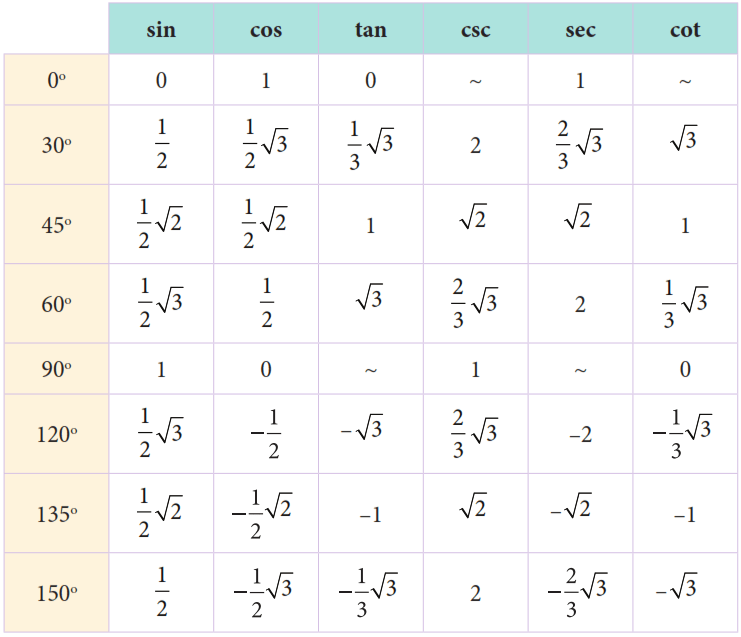
Ingat kembali nilai trigonometri pada sudut istimewa dengan menggunakan tabel trigonometri, perbandingan dan identitas trigonometri sebagai berikut.

Diketahui interval  dan
dan  , akan ditentukan interval nilai
, akan ditentukan interval nilai  yang memenuhi.
yang memenuhi.
Terlebih dahulu ubahlah  dalam bentuk pertidaksamaan sederhana.
dalam bentuk pertidaksamaan sederhana.

tentukan nilai  yang memenuhi dengan menggunakan cara mengubah ke pertidaksamaan trigonometri menjadi persamaan trigonometri.
yang memenuhi dengan menggunakan cara mengubah ke pertidaksamaan trigonometri menjadi persamaan trigonometri.

Dengan menggunakan persamaan trigonometri diperoleh sebagai berikut.

Untuk  .
.

Untuk  .
.

Sehingga nilai  yang memenuhi syarat
yang memenuhi syarat  adalah
adalah  dan
dan  .
.
Kemudian tetapkan tanda positif atau negatif yang sesuai dengan  pada garis bilangan.
pada garis bilangan.
Karena penyebutnya tidak boleh nol maka  , sehingga batas-batas pada garis bilangan adalah
, sehingga batas-batas pada garis bilangan adalah  .
.
Tanda positif dan negatif pada garis bilangan dapat diperoleh sebagai berikut.
*Menentukan tanda di antara  dan
dan  pilih sudut
pilih sudut  (gunakan kalkulator).
(gunakan kalkulator).

Karena hasilnya bernilai negatif, maka tanda di antara  dan
dan  adalah negatif.
adalah negatif.
*Menentukan tanda di antara  dan
dan  pilih sudut
pilih sudut  .
.

Karena hasilnya bernilai positif, maka tanda di antara  dan
dan  adalah positif.
adalah positif.
*Menentukan tanda di antara  dan
dan  pilih sudut
pilih sudut  .
.

Karena hasilnya bernilai negatif, maka tanda di antara  dan
dan  adalah negatif.
adalah negatif.
*Menentukan tanda di antara  dan
dan  pilih sudut
pilih sudut  (gunakan kalkulator).
(gunakan kalkulator).

Karena hasilnya bernilai positif, maka tanda di antara  dan
dan  adalah positif.
adalah positif.
*Menentukan tanda di antara  dan
dan  pilih sudut
pilih sudut  .
.

Karena hasilnya bernilai negatif, maka tanda di antara  dan
dan  adalah negatif.
adalah negatif.
*Menentukan tanda di antara  dan
dan  pilih sudut
pilih sudut  .
.

Karena hasilnya bernilai positif, maka tanda di antara  dan
dan  adalah positif.
adalah positif.
Sehingga diperoleh gambar garis bilangan seperti berikut.

Karena tanda pertidaksamaan adalah  , maka daerah yang memenuhi pertidaksamaan
, maka daerah yang memenuhi pertidaksamaan  adalah yang bertanda negatif , yaitu
adalah yang bertanda negatif , yaitu  atau
atau  atau
atau  .
.
Jadi, diperoleh himpunan penyelesaiannya dari pertidaksamaan  adalah
adalah  .
.



















