Jika luas daerah di kuadran II yang dibatasi oleh sumbu- y dan kurva y = x 2 tetapi dibawah garis y = ( 2 b − 3 ) x + 6 b dengan b > 2 3 ​ adalah 27 , maka b = … (UTBK 2021)

Pembahasan

Pertama-tama, perlu ditentukan posisi garis y = ( 2 b − 3 ) x + 6 b untuk mengetahui luas daerah pada soal. Untukmenentukan posisi garis y = ( 2 b − 3 ) x + 6 b terhadap kurva y = x 2 dapat dilihat melalui titik potong dari garis dan kurva tersebut sebagai berikut: x 2 x 2 0 0 0 0 ​ = = = = = = ​ ( 2 b − 3 ) x + 6 b 2 b x − 3 x + 6 b − x 2 + 2 b x − 3 x + 6 b − ( x 2 + ( 3 − 2 b ) x − 6 b ) − ( x + 3 ) ( x − 2 b ) ( x + 3 ) ( x − 2 b ) ​ Dari hasil pemfaktoran diperoleh x = − 3 dan x = 2 b . Hal ini berarti untuk x = − 3 maka y ​ = = = ​ x 2 ( − 3 ) 2 9 ​ Titik potong garis dan kurva tersebut adalah ( − 3 , 9 ) . Selain itu dapat diperoleh pula titik potong garis y = ( 2 b − 3 ) x + 6 b dengan sumbu- y dan sumbu- x , sebagai berikut: Untuk x = 0 (titik potong dengan sumbu- y ) maka y ​ = = = ​ ( 2 b − 3 ) x + 6 b ( 2 b − 3 ) ⋅ 0 + 6 b 6 b ​ Titik potong garis y dengan sumbu- y adalah ( 0 , 6 b ) . Untuk y = 0 (titik potong dengansumbu- x ) maka y 0 − 6 b 2 b − 3 − 6 b ​ ​ = = = = ​ ( 2 b − 3 ) x + 6 b ( 2 b − 3 ) x + 6 b ( 2 b − 3 ) x x ​ Titik potong garis y dengan sumbu- x adalah ( 2 b − 3 − 6 b ​ , 0 ) . 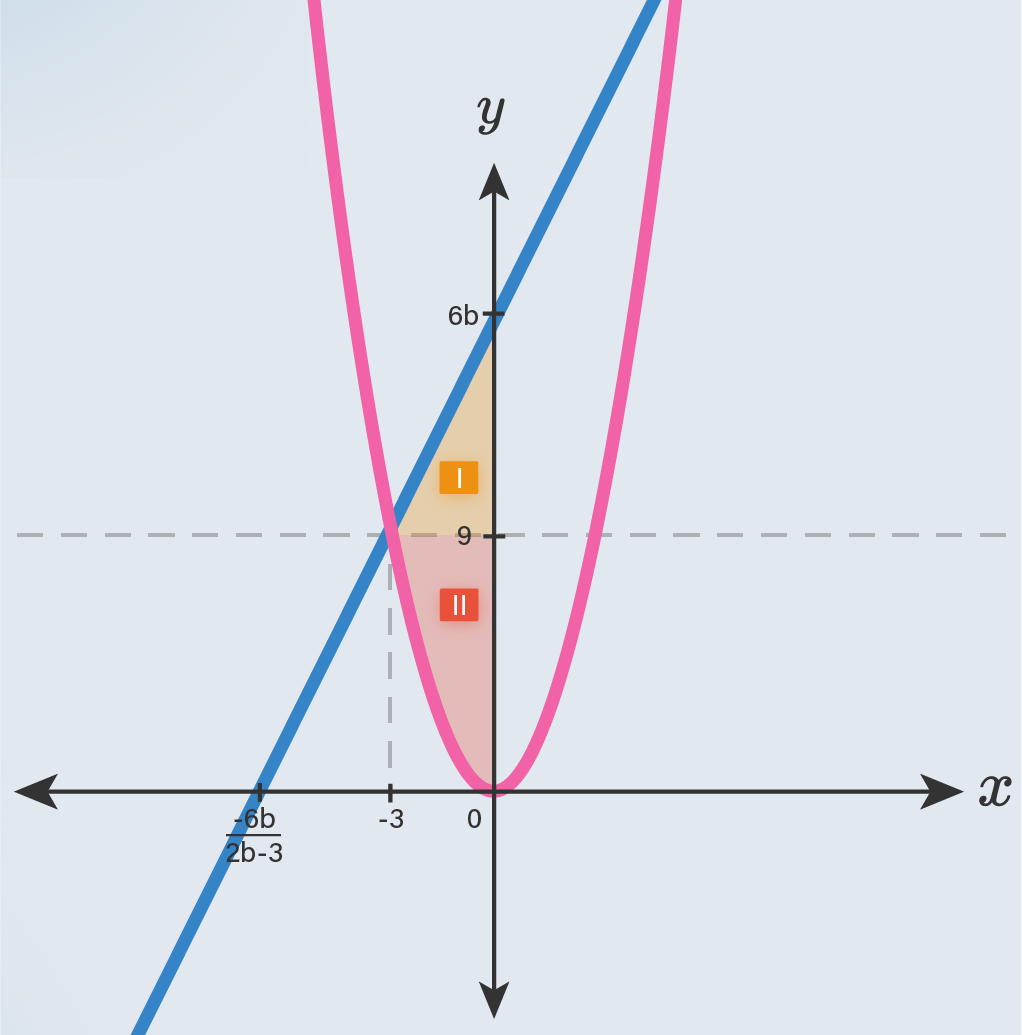Berikut adalah gambaran dari daerah yang dibentuk oleh kurva y = x 2 , sumbu- y dangaris y = ( 2 b − 3 ) x + 6 b pada kuadran II: Untuk menentukan nilai b dapat dengan menghitung masing-masing luas daerah. Luas daerah tersebut dapat dihitung menggunakan luas segitiga untuk daerah 1 dan menggunakan konsep integral luas daerah di kurva untuk daerah 2. Akan dihitung luas daerah 1. Ingat rumus luas segitiga: L segitiga ​ = 2 1 ​ ⋅ alas ⋅ tinggi Dari gambar terlihat bahwa, alas segitiga = 3 dan tinggi segitiga = 6 b − 9 maka L daerah 1 ​ ​ = = = ​ L segitiga ​ 2 1 ​ ⋅ 3 ⋅ ( 6 b − 9 ) 2 3 ​ ( 6 b − 9 ) ​ Selanjutnya, untuk mencari luas daerah 2 dapat dengan menggunakan konsep luas daerah yang dibatasi oleh fungsi f ( x ) = a x 2 + b x + c dan sumbu- x . Namun karena luas daerah yang ingin dicari hanya berupa setengah luas daerah yang dibatasi oleh y = x 2 dan garis y = 9 maka dapat dimisalkan jarak titik ( − 3 , 9 ) dengan ( 0 , 9 ) = p = 3 jarak titik ( 0 , 0 ) dengan ( 0 , 9 ) = q = 9 Hal ini berarti luas daerah 2 adalah L daerah 2 ​ ​ = = = ​ 3 2 ​ ⋅ ( p ⋅ q ) 3 2 ​ ⋅ ( 3 ⋅ 9 ) 18 ​ Telah diketahui luas seluruh daerah tersebut adalah 27 hal ini berarti: L total ​ 27 ( 27 − 18 ) 3 2 ​ 6 + 9 b b ​ = = = = = = ​ L daerah 1 ​ + L daerah 2 ​ 2 3 ​ ( 6 b − 9 ) + 18 6 b − 9 6 b 6 15 ​ 2 5 ​ ​ Dengan demikian, nilai b = 2 5 ​ . Oleh karena itu, jawaban yang tepat adalah B.