Pertanyaan

In problem a to d, match the solution region of each system of linear inequalities with one of the four regions shown in the figure. d. { x + 2 y ≤ 8 3 x − 2 y ≤ 0

In problem a to d, match the solution region of each system of linear inequalities with one of the four regions shown in the figure.

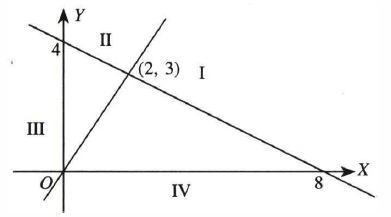
d. ${x + 2 y \leq 8 3 x - 2 y \leq 0$

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

I. Sutiawan

Master Teacher

Mahasiswa/Alumni Universitas Pasundan

Jawaban terverifikasi

Jawaban

penyelesaian dari sistem pertidaksamaan linear tersebu adalah daerah III seperti pada gambar di atas.

Pembahasan

Langkah pertama adalah kita gambargaris x + 2 y = 8 dan 3 x − 2 y = 0 seperti pada gambar berikut: Untuk menentukan daerah penyelesaian dua pertidaksamaan tersebut, kita gunakan uji titik untuk masing- masing pertidaksamaan seperti berikut: Daerah pertidaksamaan x + 2 y ≤ 8 . Pada gambar, garis x + 2 y = 8 terbagi menjadi 2 daerah yaitu daerah di atas garis dan di bawah garis, titik ( 0 , 0 ) terletak di bawah garis, sehingga melalui uji titik, daerah penyelesaian x + 2 y ≤ 8 adalah: 0 + 2 ( 0 ) 0 ≤ ≤ 8 8 Karena menghasilkan bentuk yang benar, maka daerah penyelesaiannya adalahdaerah di bawahgaris x + 2 y = 8 . Daerah pertidaksamaan 3 x − 2 y ≤ 0 . Pada gambar, garis 3 x − 2 y = 0 terbagi menjadi 2 daerah yaitu daerah di atas garis dan di bawah garis, titik ( 1 , 0 ) terletak di bawah garis, sehingga melalui uji titik, daerah penyelesaian 3 x − 2 y ≤ 0 adalah: 3 ( 1 ) − 2 ( 0 ) 1 ≤ ≤ 0 0 Karena menghasilkan bentuk yang salah, maka daerah penyelesaiannya bukan daerah bawah melainkan daerah di atas garis 3 x − 2 y = 0 . Sehingga, daerah penyelesaian dari keduapertidaksamaan tersebut adalah irisan daerah dari keduanya, yaitu: Dengan demikian, penyelesaian dari sistem pertidaksamaan linear tersebu adalah daerah III seperti pada gambar di atas.

Langkah pertama adalah kita gambar garis $x + 2 y = 8$ dan $3 x - 2 y = 0$ seperti pada gambar berikut:

Untuk menentukan daerah penyelesaian dua pertidaksamaan tersebut, kita gunakan uji titik untuk masing- masing pertidaksamaan seperti berikut:

Daerah pertidaksamaan $x + 2 y \leq 8$ .

Pada gambar, garis $x + 2 y = 8$ terbagi menjadi 2 daerah yaitu daerah di atas garis dan di bawah garis, titik $(0, 0)$ terletak di bawah garis, sehingga melalui uji titik, daerah penyelesaian $x + 2 y \leq 8$ adalah:

$0 + 2 (0) 0 \leq \leq 88$

Karena menghasilkan bentuk yang benar, maka daerah penyelesaiannya adalah daerah di bawah garis $x + 2 y = 8$ .

Daerah pertidaksamaan $3 x - 2 y \leq 0$ .

Pada gambar, garis $3 x - 2 y = 0$ terbagi menjadi 2 daerah yaitu daerah di atas garis dan di bawah garis, titik $(1, 0)$ terletak di bawah garis, sehingga melalui uji titik, daerah penyelesaian $3 x - 2 y \leq 0$ adalah:

$3 (1) - 2 (0) 1 \leq \leq 00$

Karena menghasilkan bentuk yang salah, maka daerah penyelesaiannya bukan daerah bawah melainkan daerah di atas garis $3 x - 2 y = 0$ .

Sehingga, daerah penyelesaian dari kedua pertidaksamaan tersebut adalah irisan daerah dari keduanya, yaitu:

Dengan demikian, penyelesaian dari sistem pertidaksamaan linear tersebu adalah daerah III seperti pada gambar di atas.

Buka akses jawaban yang telah terverifikasi

Yah, akses pembahasan gratismu habis

atau

Dapatkan jawaban pertanyaanmu di AiRIS. Langsung dijawab oleh bestie pintar

Tanya Sekarang

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

0.0 (0 rating)

Pertanyaan serupa

Gambarlah daerah penyelesaian sistem pertidaksamaan berikut 2 x + 3 y x + y x y ≥ ≤ > ≥ 12 5 0 0

4.8

Jawaban terverifikasi

Lukiskan DHP setiap SPtLDV berikut. Apakah DHP yang terbentuk merupakan daerah tertutup? Jika ya, hitunglah luas daerah tertutup tersebut dan cari koordinat setiap titik pojok yang membatasi daerah te...

0.0

Jawaban terverifikasi

Tentukan nilai minimum dari fungsi objektif f ( x , y ) = 40 x + 30 y yang memenuhi sistem pertidaksamaan 2 x + y ≥ 11 ; x + 2 y ≥ 10 ; x ≥ 0 ; dan y ≥ 0 untuk x , y ∈ R .

5.0

Jawaban terverifikasi

Diketahui suatu sistem pertidaksamaan ⎩ ⎨ ⎧ − 3 x + 2 y ≤ 6 x + 2 y ≥ − 2 x ≤ 2 y ≤ 3 a. Gambarkan daerah penyelesaiannya pada bidang koordinat kartesius. b. Tentukan luas daerah penyeles...

4.8

Jawaban terverifikasi

Tentukan daerah himpunan penyelesaian dari sistem pertidaksamaan x + 3 y ≥ 6 ; 2 x + y ≥ 7 ; x + y ≤ 14 ; 0 ≤ x ≤ 9 ; dan y ≥ 0 untuk x , y ∈ R dan tentukan nilai maksimum dan minimum dari fungsi obje...

5.0

Jawaban terverifikasi

Tanya ke AiRIS

Yuk, cobain chat dan belajar bareng AiRIS, teman pintarmu!

Chat AiRIS