Cara I :
Misalkan  , dari
, dari  didapatkan perhitungan sebagai berikut.
didapatkan perhitungan sebagai berikut.

Bentuk positif dari bentuk di ruas kanan adalah  dan nilai sudut lancip.
dan nilai sudut lancip. yang memenuhi adalah
yang memenuhi adalah  .
.
Perhatikan gambar berikut!
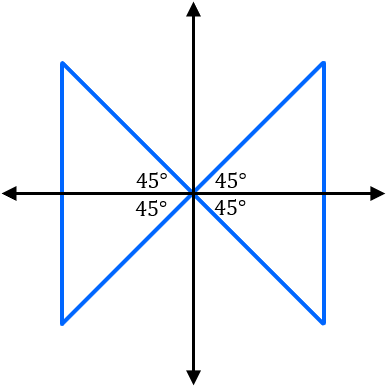
Dapat diperhatikan bahwa  bernilai negatif.
bernilai negatif.
Akibatnya,  berada di kuadran II atau III.
berada di kuadran II atau III.
Perhatikan gambar berikut!
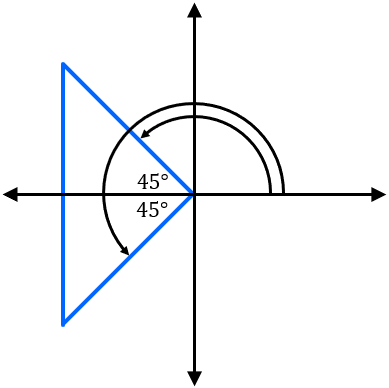
Dari sudut di kuadran II didapat  .
.
Dari sudut di kuadran III didapat  .
.
Dalam hal ini didapatkan penyelesaian umumnya adalah  dan
dan  dengan
dengan  adalah bilangan bulat.
adalah bilangan bulat.
Pada soal diberikan syarat  .
.
Perlu diperiksa terlebih dahulu penyelesaian umum yang pertama, yaitu  .
.
Dari penyelesaian umum ini didapat perhitungan sebagai berikut.

Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  memenuhi syarat yang diberikan.
memenuhi syarat yang diberikan.
Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  tidak memenuhi syarat yang diberikan sehingga nilai
tidak memenuhi syarat yang diberikan sehingga nilai  tidak mungkin lebih kecil lagi.
tidak mungkin lebih kecil lagi.
Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  memenuhi syarat yang diberikan.
memenuhi syarat yang diberikan.
Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  tidak memenuhi syarat yang diberikan sehingga nilai
tidak memenuhi syarat yang diberikan sehingga nilai  tidak mungkin lebih besar lagi.
tidak mungkin lebih besar lagi.
Dengan demikian, dari  didapat nilai
didapat nilai  yang memenuhi syarat adalah
yang memenuhi syarat adalah  dan
dan  .
.
Kemudian, perlu diperiksa penyelesaian umum yang kedua, yaitu  .
.
Dari penyelesaian umum ini didapat perhitungan sebagai berikut.

Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  memenuhi syarat yang diberikan.
memenuhi syarat yang diberikan.
Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  tidak memenuhi syarat yang diberikan sehingga nilai
tidak memenuhi syarat yang diberikan sehingga nilai  tidak mungkin lebih kecil lagi.
tidak mungkin lebih kecil lagi.
Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  memenuhi syarat yang diberikan.
memenuhi syarat yang diberikan.
Untuk  diperoleh
diperoleh  .
.
Dapat diperhatikan bahwa  tidak memenuhi syarat yang diberikan sehingga nilai
tidak memenuhi syarat yang diberikan sehingga nilai  tidak mungkin lebih besar lagi.
tidak mungkin lebih besar lagi.
Dengan demikian, dari  didapat nilai
didapat nilai  yang memenuhi syarat adalah
yang memenuhi syarat adalah  dan
dan  .
.
Oleh karena itu, himpunan nilai  yang memenuhi
yang memenuhi  dengan
dengan  adalah
adalah  .
.
Cara II :
Ingat bahwa  sehingga diperoleh
sehingga diperoleh  .
.
Persamaan  terpenuhi oleh
terpenuhi oleh

dan

dengan  .
.
Perhatikan perhitungan sebagai berikut.

Jika  , maka
, maka  . Nilai tersebut tidak memenuhi syarat
. Nilai tersebut tidak memenuhi syarat  sehingga untul nilai
sehingga untul nilai  makin kecil pasti tidak memenuhi syarat
makin kecil pasti tidak memenuhi syarat  juga.
juga.
Jika  , maka
, maka  . Nilai tersebut memenuhi syarat
. Nilai tersebut memenuhi syarat  .
.
Jika  , maka
, maka  . Nilai tersebut memenuhi syarat
. Nilai tersebut memenuhi syarat  .
.
Jika  , maka
, maka  . Nilai tersebut tidak memenuhi syarat
. Nilai tersebut tidak memenuhi syarat  sehingga untuk nilai
sehingga untuk nilai  makin besar pasti tidak memenuhi syarat
makin besar pasti tidak memenuhi syarat  juga.
juga.
Selanjutnya, diperoleh perhitungan sebagai berikut.

Jika  , maka
, maka  . Nilai tersebut tidak memenuhi syarat
. Nilai tersebut tidak memenuhi syarat  sehingga untuk nilai
sehingga untuk nilai  makin kecil pasti tidak memenuhi syarat
makin kecil pasti tidak memenuhi syarat  juga.
juga.
Jika  , maka
, maka  . Nilai tersebut memenuhi syarat
. Nilai tersebut memenuhi syarat  .
.
Jika  , maka
, maka  . Nilai tersebut memenuhi syarat
. Nilai tersebut memenuhi syarat  .
.
Jika  , maka
, maka  . Nilai tersebut memenuhi syarat
. Nilai tersebut memenuhi syarat  sehingga untuk nilai
sehingga untuk nilai  makin besar pasti tidak memenuhi syarat
makin besar pasti tidak memenuhi syarat  juga.
juga.
Dengan demikian, diperoleh himpunan nilai  yang memenuhi yaitu
yang memenuhi yaitu  .
.
Jadi, jawaban yang tepat adalah A.

















