Pertanyaan

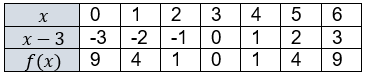
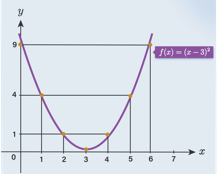
Grafik fungsi f ( x ) = ( x − 3 ) 2 a. Buatlah tabel yang memuat hubungan nilai x dan nilai f ( x ) ! b. Gambarlah grafik fungsi f ( x ) = ( x − 3 ) 2 pada bidang koordinat di samping! c. Tentukan koordinat titik balik atau titik puncak pada grafik yang telah kalian buat!

Grafik fungsi $f (x) = (x - 3)^{2}$
a. Buatlah tabel yang memuat hubungan nilai $x$ dan nilai $f (x)$ !
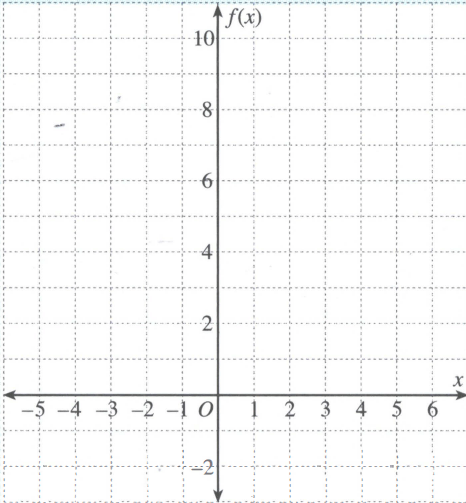
b. Gambarlah grafik fungsi $f (x) = (x - 3)^{2}$ pada bidang koordinat di samping!
c. Tentukan koordinat titik balik atau titik puncak pada grafik yang telah kalian buat!

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

L. Rante

Master Teacher

Mahasiswa/Alumni Universitas Negeri Makassar

Jawaban terverifikasi

Pembahasan

a) Tabelhubungan nilai x dan nilai f ( x ) b) Berdasarkan tabel tersebut, dapat dibuatgrafik fungsi f ( x ) = ( x − 3 ) 2 seperti di bawah ini c) Berdasarkan gambar tersebut, koordinat titik balik atau titik puncak dari f ( x ) = ( x − 3 ) 2 adalah ( 3 , 0 ) .

a) Tabel hubungan nilai $x$ dan nilai $f (x)$

b) Berdasarkan tabel tersebut, dapat dibuat grafik fungsi $f (x) = (x - 3)^{2}$ seperti di bawah ini

c) Berdasarkan gambar tersebut, koordinat titik balik atau titik puncak dari $f (x) = (x - 3)^{2}$ adalah $(3, 0)$ .

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

4.1 (6 rating)

Anjayani

Terimakasih bos,soalnya mirip punya saya tapi banyak rubahan,anda beri awalan yg Bagus pada saya👍

Pisgor Bandung

Makasih ❤️

Pertanyaan serupa

Diketahui fungsi f : R → R dan f ( x ) = x 2 + 2 x − 3. b . Gambarkan grafik fungsi tersebut.

4.8

Jawaban terverifikasi

Gambarlah sketsa grafik fungsi berikut! a. f ( x ) = x 2 − 3 x + 2

3.6

Jawaban terverifikasi

Fungsi f ( x ) = x 2 − 9 x + 18 memiliki daerah asal 2 ≤ x ≤ 7 , x ∈ R ( bilangan real ) . a. Buatlah tabelhubungan nilai x dan f ( x ) ! b. Gambarlah grafik f ( x ) = x 2 − 9 x + 18 ! c. Tentukan ...

137

4.6

Jawaban terverifikasi

Diketahui suatu fungsi memiliki bentuk fungsi m ( x ) = 5 x 2 + 3 x − 4 dan x = { bilangan prima kurang dari 15 } . Buatlah tabel nilai fungsinya! Gambarlah grafik fungsinya!

0.0

Jawaban terverifikasi

Gambarkan grafik fungsi kuadrat berikut. c. f ( x ) = 2 x 2 + 3 x + 2 .

4.0

Jawaban terverifikasi