Pertanyaan

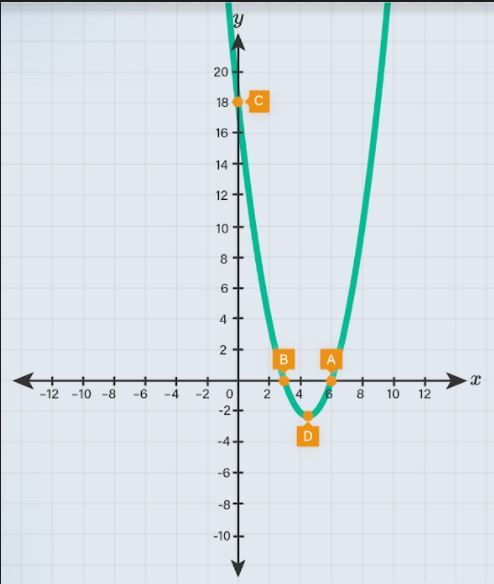
Fungsi f ( x ) = x 2 − 9 x + 18 memiliki daerah asal 2 ≤ x ≤ 7 , x ∈ R ( bilangan real ) . a. Buatlah tabelhubungan nilai x dan f ( x ) ! b. Gambarlah grafik f ( x ) = x 2 − 9 x + 18 ! c. Tentukan persamaan sumbu simetrinya! d. Tentukan nilai minimumnya!

Fungsi $f (x) = x^{2} - 9 x + 18$ memiliki daerah asal $2 \leq x \leq 7, x \in R (bilangan real) .$
a. Buatlah tabel hubungan nilai $x dan f (x)$ !
b. Gambarlah grafik $f (x) = x^{2} - 9 x + 18$ !
c. Tentukan persamaan sumbu simetrinya!
d. Tentukan nilai minimumnya!

Ikuti Tryout SNBT & Menangkan E-Wallet 100rb

Habis dalam

Klaim

A. Acfreelance

Master Teacher

Jawaban terverifikasi

Pembahasan

Ingat persamaan umum fungsi kuadrat adalah : a x 2 + b x + c = 0 a. Tabel hubungan nilai x dan f ( x ) c. Persamaan sumbu simetri x = 2 a − b = 2 ⋅ 1 − ( − 9 ) = 2 9 d. Nilai minimum y = − 4 a b 2 − 4 ⋅ a ⋅ c = − 4 ⋅ 1 ( − 9 ) 2 − 4 ⋅ 1 ⋅ 18 = − 4 9 b. Gambar grafik 1. Menentukan titik potong terhadap sumbu x . x 2 − 9 x + 18 = 0 ( x − 6 ) ( x − 3 ) = 0 x = 6 atau x = 3 Maka titik potong di sumbu x adalah ( 6 , 0 ) dan ( 3 , 0 ) . 2. Menentukan titik potong terhadap sumbu y. Grafik fungsi kuadrat memotong sumbu y apabila f ( 0 ) . f ( x ) = x 2 − 9 x + 18 f ( 0 ) = 0 2 − 9 ( 0 ) + 18 f ( 0 ) = 18 Grafik memotong sumbu-y di titik ( 0 , 18 ) 5. Menentukan koordinat titik balik . Koordinat titik balik adalah nilai sumbu simetri dan niai minimum, sehingga koordinat titik balik adalah: ( 2 9 , 4 − 9 ) Dengan demikian,sketsa grafik fungsi adalah sebagai berikut:

Ingat persamaan umum fungsi kuadrat adalah : $a x^{2} + b x + c = 0$

a. Tabel hubungan nilai $x dan f (x)$

c. Persamaan sumbu simetri

$x = \frac{- b}{2 a} = \frac{- ( - 9 )}{2 \cdot 1} = \frac{9}{2}$

d. Nilai minimum

$y = \frac{b ^{2} - 4 \cdot a \cdot c}{- 4 a} = \frac{( - 9 ) ^{2} - 4 \cdot 1 \cdot 18}{- 4 \cdot 1} = - \frac{9}{4}$

b. Gambar grafik

1. Menentukan titik potong terhadap sumbu $x$ .

$x^{2} - 9 x + 18 = 0 (x - 6) (x - 3) = 0 x = 6 atau x = 3$

Maka titik potong di sumbu x adalah $(6, 0) dan (3, 0)$ .

2. Menentukan titik potong terhadap sumbu y.

Grafik fungsi kuadrat memotong sumbu y apabila $f (0)$ .

$f (x) = x^{2} - 9 x + 18 f (0) = 0^{2} - 9 (0) + 18 f (0) = 18$

Grafik memotong sumbu-y di titik $(0, 18)$

5. Menentukan koordinat titik balik .
Koordinat titik balik adalah nilai sumbu simetri dan niai minimum, sehingga koordinat titik balik adalah:

$(\frac{9}{2}, \frac{- 9}{4})$

Dengan demikian, sketsa grafik fungsi adalah sebagai berikut:

Perdalam pemahamanmu bersama Master Teacher
di sesi Live Teaching, GRATIS!

100

4.6 (20 rating)

Zeyn

Bantu banget

aisyah mardian

The best Bantu banget

Aseline Bilqisthi

Pembahasan lengkap banget Bantu banget Makasih ❤️

Alvin

Jawaban tidak sesuai

kayla navrilda yusna

Pembahasan tidak lengkap

Pertanyaan serupa

Sebuah persegi panjang berukuran panjang x cm dan Iebar ( 8 − x ) cm . L(x) menyatakan fungsi untuk luas persegi panjang tersebut. a. Buatlah model matematika untuk L(x) ! b. Buatlah sketsa grafik...

4.5

Jawaban terverifikasi

Buatlah tabel fungsi, grafik fungsi kuadrat dan tentukan unsur - unsur grafiknya untuk fungsi kuadrat berikut. y = x 2 + 4 x + 2

0.0

Jawaban terverifikasi

Gambarlah sketsa grafik fungsi berikut! a. f ( x ) = x 2 − 3 x + 2

3.6

Jawaban terverifikasi

Sebutkan titik potong terhadap sumbu X fungsi f ( x ) = x 2 + 8 x + 12 dan gambarkan posisi grafik terhadap sumbu Y.

5.0

Jawaban terverifikasi

Diketahui fungsi kuadrat f ( x ) = − x 2 − 4 x + 12 . 1. Tentukan titik potong fungsi dengan sumbu X! 2.Tentukan titik potong fungsi dengan sumbu Y! 3.Tentukan titik puncak/titik baliknya! ...

4.2

Jawaban terverifikasi